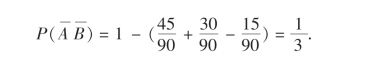概率的公理化定义
古典概率与几何概率的定义都是以样本点出现的“等可能性”作为基础，因此它们的适用范围有很大的局限性.统计概率的定义也存在理论和应用上的缺陷.因此，对一般随机现象明确地定义概率，对于概率论的研究是十分必要的.由前面的讨论知道，统计概率、古典概率、几何概率的定义，其背景虽然不同，但它们却具有一些共同的性质，即概率的非负性、规范性以及有限可加性.另外，几何概率还具有可列可加性.这就说明这些性质是概率的最基本的性质，由此人们想到直接用这些性质来作为一般的概率定义，这就是下面的概率公理化定义.
1.概率的定义
定义4 设E是随机试验，Ω是它的样本空间.对于E的每一个事件A对应着一个实数，记为P（A），如果它满足下列条件，就称P（A）为事件A的概率：
（i）非负性：对任一事件A，有
（ii）规范性：
（iii）可列可加性：对于互不相容的事件Ak（k=1，2，…，n，…）有
2.概率的性质
定理1 由定义4所定义的概率P（A），具有如下的性质：
（iii）对于事件A和B，如果A⊂B则有
（iv）对于任意两事件A，B有
得
即
（1.9）得证；由概率的非负性（1.4），P（B-A）≥0，即
（iv）因A∪B=A∪（B-AB），且A（B-AB）=
，AB⊂B，利用（1.8）和（1.9）得
推论1 对任一事件A，有
即
推论2 （一般加法公式）对于任意n个事件A1，A2，…，An，有
其中
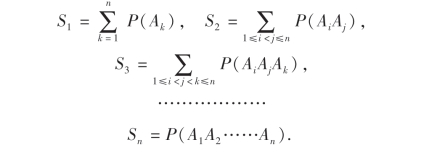
其证明可用数学归纳法，这里略.
例15 设事件A，B的概率分别为
，求在下列三种情况下
的值：
（1）A与B互不相容；
（2）A⊂B；
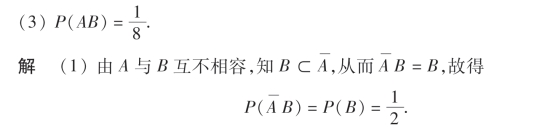
（2）当A⊂B时，
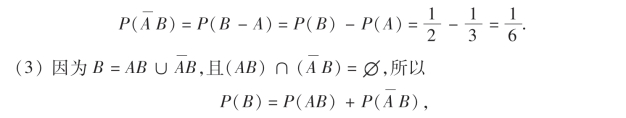
即
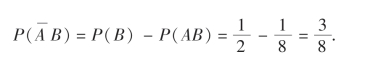
例16 在10～99的整数中随机地取一个数，求取到的整数既不能被2整除，又不能被3整除的概率.
解 设A为事件“取到的数能被2整除”，B为事件“取到的数能被3整除”，则所求概率为
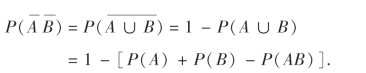
注意，一个数同时能被2和3整除，相当于该数能被6整除.由于10～99的整数有90个，其中能被2整除的有45个，能被3整除的有30个，能被6整除的有15个，故
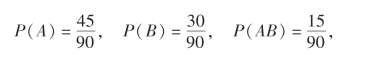
于是得
