四、统计量

四、统计量

样本是进行统计推断的依据，在应用时，往往不是直接使用样本进行统计推断，而是针对不同的问题构造样本的适当函数，利用这些样本的函数进行统计推断.这些适当的函数就是统计量.

定义3 设X1，X2，…，Xn是来自总体X的一个样本，g（X1，X2，…，Xn）是X1，X2，…，Xn的连续函数，若g中不含未知参数，则称g（X1，X2，…，Xn）是一个统计量.

例如，设总体X～N（μ，σ2），μ已知，σ未知，X1，X2，…，Xn是来自总体X的一个样本，则

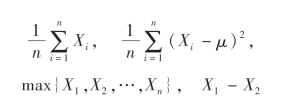
都是统计量.而

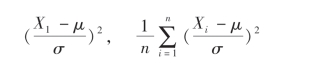
不是统计量.

因为X1，X2，…，Xn都是随机变量，而统计量g（X1，X2，…，Xn）是随机变量的函数，因此统计量是一个随机变量.设x1，x2，…，xn是相应于样本X1，X2，…，Xn的样本值，则称g（x1，x2，…，xn）是g（X1，X2，…，Xn）的观察值.

下面介绍几个常用的重要统计量：它们的观察值分别为

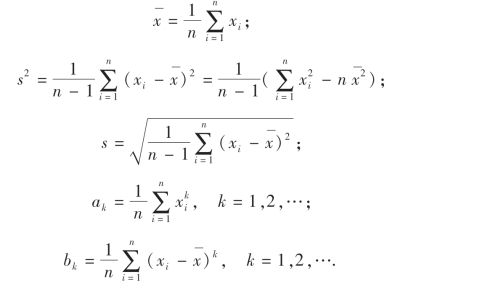
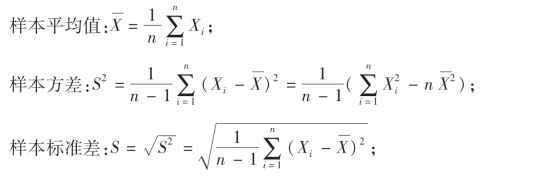
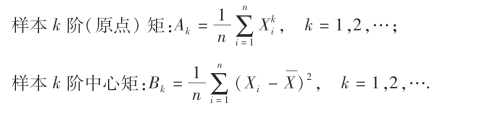
这些观察值仍分别称为样本均值、样本方差、样本标准差、样本k阶（原点）矩以及样本k阶中心矩.

根据样本均值和样本方差的定义容易推得：

（1）若Yi=Xi-c（i=1，2，…，n；c为常数），则

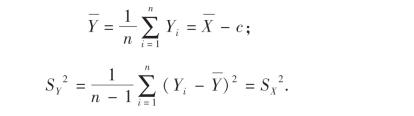
（2）若总体的期望和方差存在且E（X）=μ，D（X）=σ2，则

设总体X的k阶矩E（Xk）=μk存在，X1，X2，…，Xn是来自总体X的样本，根据第五章的大数定律可得：对任意给定的ε＞0有

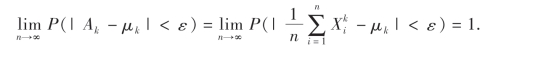
这就说明，只要n足够大，就能以充分的把握保证：