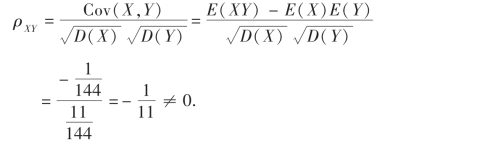相关系数的定义和性质
由协方差的定义可知,Cov(X,Y)反映了X和Y相互间的关联程度,但它还受X与Y自身取值的影响.例如,当X与Y同时增大k倍时,kX与kY之间的相互联系和X与Y之间的相互联系应该是一样的,然而反映这种联系的协方差却增大了k2倍,即有

定义5 设(X,Y)是一个二维随机变量,且D(X)>0,D(Y)>0,则称
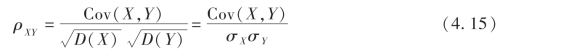
为X与Y的相关系数(或标准协方差).
相关系数的性质:
性质1 设ρXY为随机变量X和Y的相关系数,则|ρXY|≤1.
证
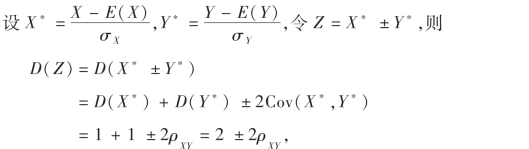
由于方差非负,故2±2ρXY≥0,从而有|ρXY|≤1.
性质2 |ρXY|=1的充要条件是存在常数a≠0,b使
![]()
证 充分性:若Y=aX+b,则
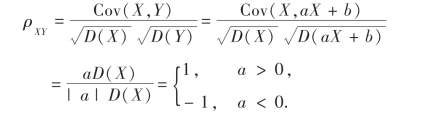
即Y与X具有线性关系时|ρXY|=1.
必要性:当ρXY=1时,令Z=Y*-X*,则
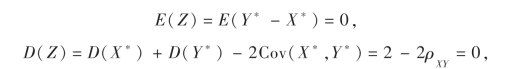
由方差的性质4可知,存在常数C=E(Z)=0,则
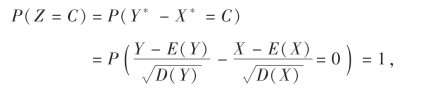
即
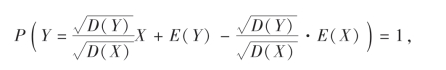
令
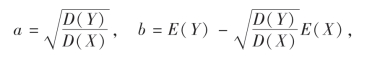
则

这个性质告诉我们:
(1)相关系数ρXY的大小是X与Y之间线性关系的一种度量.
(2)如果ρXY=0,我们称X,Y不相关;不相关表示X,Y之间不存在线性关系,但不排除有其他函数关系.
(3)当|ρXY|=1时,则称X与Y完全线性相关.
(4)如果|ρXY|<1,我们称X与Y存在“一定程度”的线性关系.|ρXY|越接近于1,则线性相关程度越强;|ρXY|越接近于0,则线性相关程度越弱.
性质3 如果随机变量X与Y相互独立,则X与Y不相关;反之则不然.
证 当X与Y相互独立时,由协方差的性质5及(4.15)可得ρXY=0,即X与Y不相关;反之则不然,见下面的反例.
例19 设X ~U(-1,1),令Y=X2,讨论X与Y的相关性及其相互独立性.
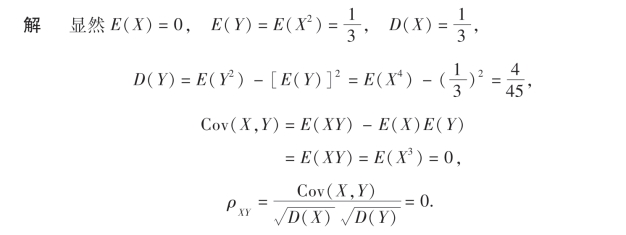
即X与Y不相关,但Y=X2,所以X与Y不独立.
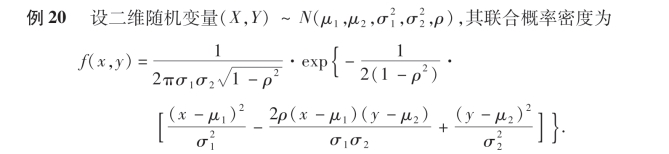
求Cov(X,Y)和ρXY,并说明在二维正态分布的情况下,不相关与独立是等价的.
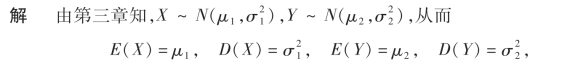
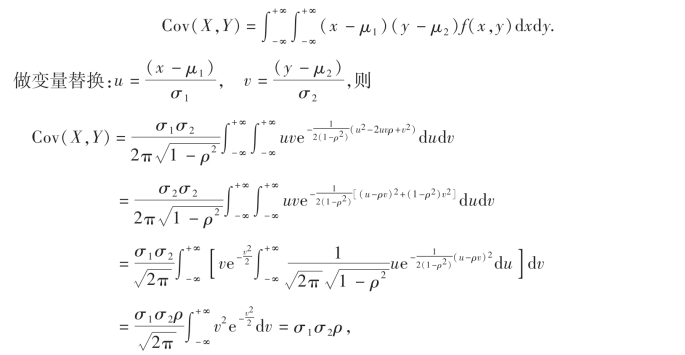
于是
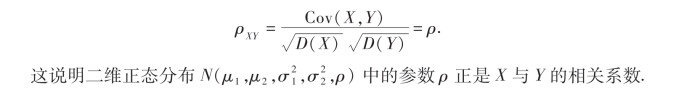
当ρXY=0时,即ρ=0,这时X与Y不相关,则
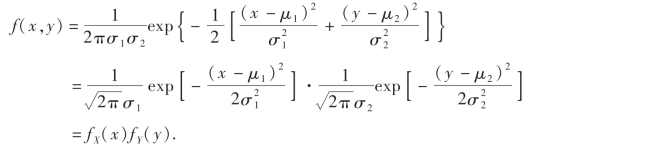
所以X与Y独立;而由相关系数的性质3,如果随机变量X与Y相互独立,则X与Y不相关,即ρXY=ρ=0;所以,在二维正态分布的情况下,不相关与独立是等价的.
例21 设二维随机变量X与Y的联合概率密度函数为
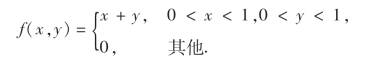
求X,Y的相关系数ρXY.
解
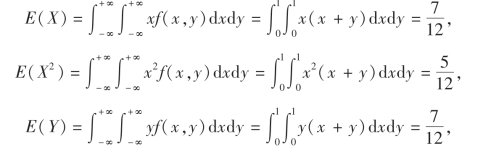
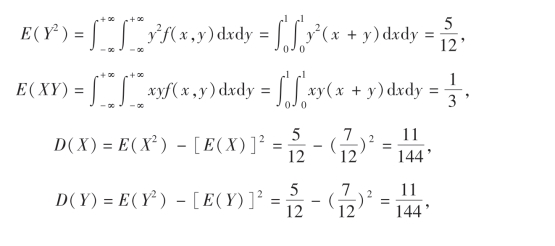
则