§5.1　切比雪夫不等式

§5.1　切比雪夫不等式

引理1（切比雪夫不等式） 对任意随机变量X，若它的数学期望E（X）=μ和方差D（X）=σ2存在，则对任意的ε＞0，有

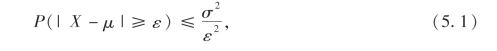
或

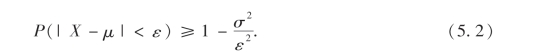
以上两个不等式均称为切比雪夫不等式.

证 设X是连续型随机变量，概率密度为f（x），事件｛|X-μ|≥ε｝表示随机变量X落在区间（μ-ε，μ+ε）之外，则

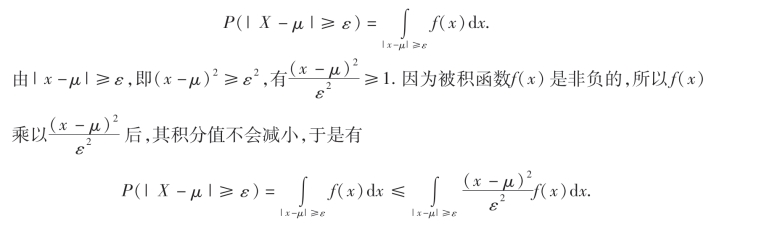
又因为被积分函数是非负函数，所以如果将积分区间|x-μ|≥ε扩大到整个数轴，则只能增大积分值，因此

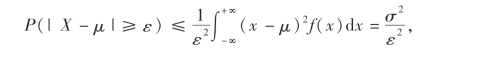
即

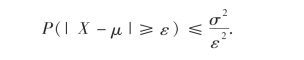
因为事件｛|X-μ|≥ε｝与｛|X-μ|＜ε｝是对立事件，所以有

由已证明的不等式（5.1），即得不等式（5.2）.

若X是离散型的随机变量，只需要在上述证明中将概率密度换成分布律，将积分号换成求和号即可.证毕.

下面通过一简单的例子说明切比雪夫不等式的应用.

例如，丢一枚均匀的硬币，试问丢900次后出现正面的次数介于400至500之间的概率是多少？

此试验属于贝努里概型，正面出现的次数服从二项分布，且

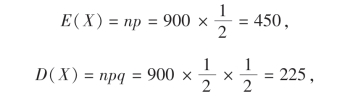
故所求概率为

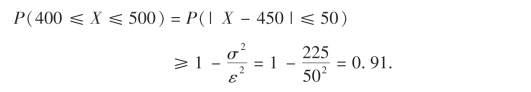
由式（5.2）知，不管X的分布是什么，对任意的正整数k都有

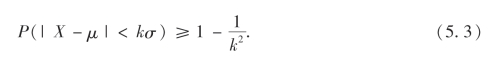
当k=3时有

但我们知道当X ～N（μ，σ2）时，

比较（5.4）式和（5.5）式知，切比雪夫不等式给出的估计是比较粗糙的.

另外用切比雪夫不等式估计概率的界时，仅当偏差区间是以μ为中心的区间时才能用.但是用切比雪夫不等式时不需要知道X服从什么分布，只要知道X的数学期望和方差就可以，因此它无论在理论研究上，还是在实际应用中都很有价值.

从切比雪夫不等式还可以看出，当方差愈小时，事件｛|X-μ|≥ε｝的概率也愈小，即方差是描述随机变量与其数学期望值离散程度的一个量，这与我们以前介绍的理论是完全一致的.