可线性化的一元非线性回归
有时两个变量之间的关系不是直线(或线性)的相关关系,而是某种曲线(或非线性)的相关关系.这类问题往往需要做曲线(或非线性)回归.对于一些非线性回归问题,与线性时一样,可以根据有关专业知识,从理论上推导出回归函数应是某种类型的函数,或者根据经验,定出函数类型,还可以根据散点图与已知类型的曲线相比较而确定函数(配曲线),然后经过适当的变量代换转化为线性问题,用线性回归的方法确定函数中的未知参数.
常用的配曲线的方法是根据散点图来确定的,即先对两个变量X和Y做n次试验观察得(xi,yi),1,2,…,n,画出散点图,根据散点图确定需要配曲线的类型.通常选择下面六类曲线之一.
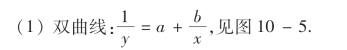
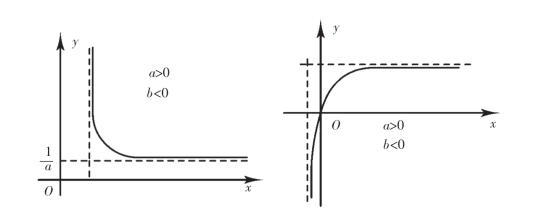
图10-5
(2)幂函数曲线:y=axb,x>0,其中a>0,见图10-6.
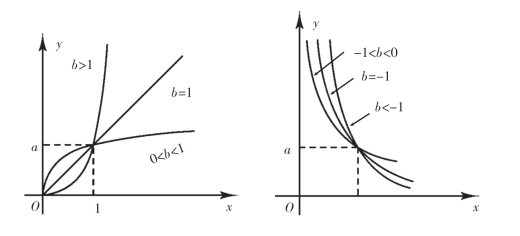
图10-6
(3)指数曲线:y=aebx,其中a>0,见图10-7.
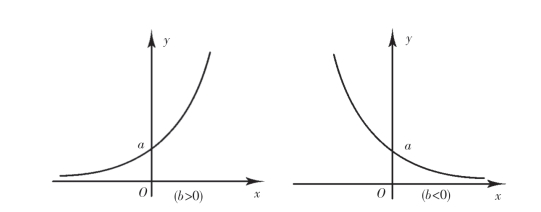
图10-7
(4)倒指数曲线:y=aeb/x,其中a>0,见图10-8.
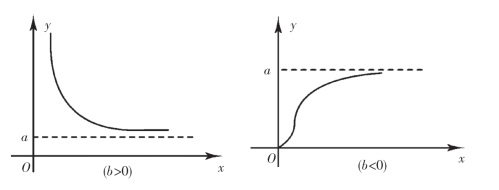
图10-8
(5)对数曲线:y=a+blnx,x>0,见图10-9.
(6)S形曲线:y=![]() ,见图10-10.
,见图10-10.
然后,再由n对试验数据确定所选曲线的未知参数a与b.采用的方法是通过变量代换把非线性回归化成线性回归,即采用非线性回归线性化的方法.下面具体介绍每类曲线线性化的具体方法.
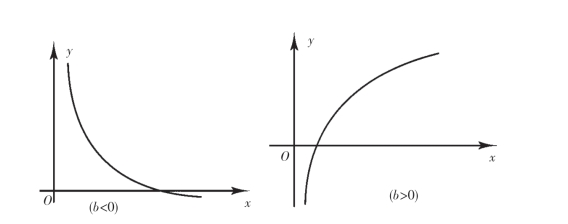
图10-9
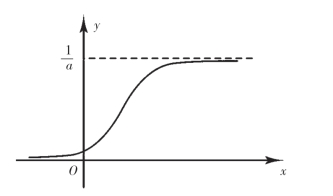
图10-10

(2)幂函数曲线:y=axb,x>0,其中a>0.

其他几类曲线线性化方法及参数求法与前两类相类似,仅仅是变量代换不同.因此,以下几类曲线仅给出变量代换.
3.指数曲线:y=aebx,其中a>0.
令v=lny,A=lna,将指数曲线方程两边取对数后即转化成
![]()
4.倒指数曲线:y=aeb/x,其中a>0.
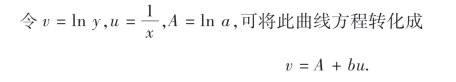
5.对数曲线:y=a+blnx,x>0.令u=lnx,则可将此曲线方程转化成

例5 已知某种树木平均胸径d与平均树高h之间的关系有如下数据:
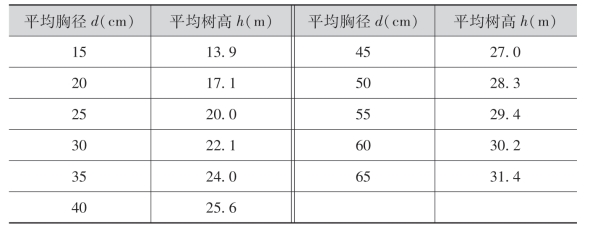
试确定平均树高与平均胸径的相关关系.
解 画出(di,hi),i=1,2,…,11的点图(图10-11).从散点图来看,选配对数曲线
![]()
令x=lnd,将di的所有数据取对数后得xi.用最小二乘法计算得
![]()
于是得h与d的回归关系为
![]()
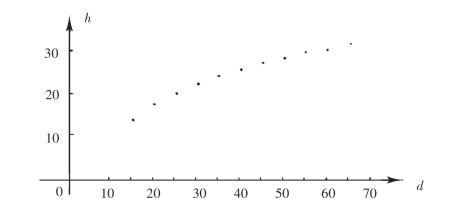
图10-11
顺便提一下,若有多种回归曲线可供选择时,选择哪一种更好呢?显然,就已知样本而言,曲线的回归值与观察值的差的平方和(即剩余平方和)QE越小,回归方程的精度就越高,因此,选择QE值较小的曲线为宜.
