习题四
1.设随机变量具有分布律为
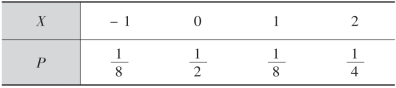
求E（X），E（X2），E（2X+3）.
2.设随机变量Y服从λ=1的指数分布，随机变量
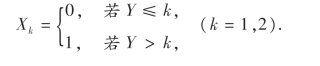
（1）求X1和X2的联合分布律； （2）E（X1+X2）.
3.盒中有k号的球k只，k=1，2，…n，从中任取一球，求所得球的号码的数学期望.
4.设X服从指数分布，其概率密度为
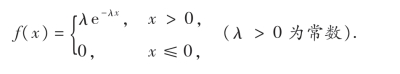
求E（X），D（X）.
5.设随机变量X的概率密度为
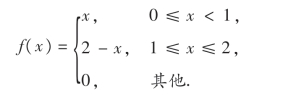
求E（X），D（X）.
6.有n把钥匙，其中有一把能打开门上的锁，设抽取钥匙是等可能性的，若把每把钥匙试开一次后除去，求试开次数X的数学期望.
7.掷2枚骰子，以X记第一枚骰子掷出的点数，Y记第二枚骰子掷出的点数，求E（X+Y）和E（XY）.
8.若X1，X2，…，Xn是相互独立的，且D（Xi）=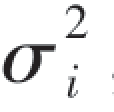
，i=1，2，…，n，试找“权”a1，a2，…，an（ai≥0，∑ai=1），使∑aiXi的方差最小.
9.设（X，Y）在区域D=｛（x，y）|0≤x≤1，0≤y≤1｝上服从均匀分布，求协方差Cov（X，Y）.
10.设二维随机变量（X，Y）的概率密度为
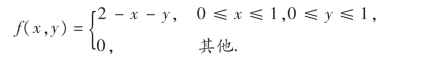
（1）问X，Y是否相互独立；
（2）求E（XY）.
11.设随机变量（X，Y）在以（0，0），（0，1），（1，0）为顶点的三角形区域上服从均匀分布，求Cov（X，Y），ρXY.
12.已知随机变量X的概率密度为
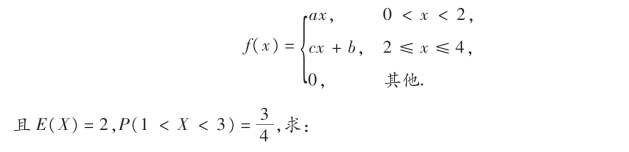
（1）a，b，c的值；
（2）E（Y）=E（eX）.
13.设（X，Y）服从二维正态分布，其概率密度为求随机变量
的数学期望.
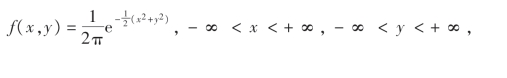
14.设随机变量X服从正态分布，它的E（X），D（X）均存在，且D（X）不等于零，标准化随机变量为
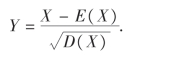
证明随机变量Y～N（0，1）.
15.设（X，Y）在圆域x2+y2≤4服从均匀分布，试问X与Y：
（1）是否独立？
（2）是否相关？
* 16.已知随机向量（X，Y）的协方差矩阵为
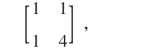
试求Z1=X-2Y与Z2=2X-Y的相关系数.