线性模型假设的检验

三、线性模型假设的检验

与一元线性回归一样，求得的回归方程是否具有实用价值.还得经过线性模型假设的检验来确定.若线性模型的假设符合实际，也就是Y与x1，x2，…，xp确有线性关系，这时回归系数b1，b2，…，bp不全为零，即需要检验假设

为此令

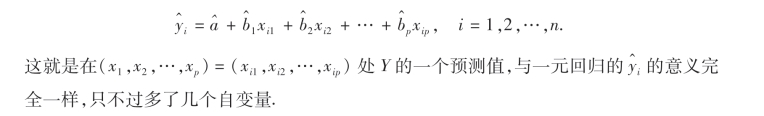
为选取统计量，仍采用方差分析方法.同样可以证明：

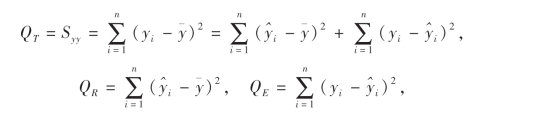
则

定理1 若b1=b2=… =bp=0，则

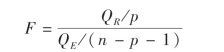
服从自由度为（p，n-p-1）的F分布.

证略.

由定理1，即得线性模型假设的检验方法.对给定的显著水平α，查表可得Fα（p，np-1），把抽样后计算的F值与之比较，若F≥Fα，则拒绝H0，认为线性回归显著；若F＜Fα，则认为线性回归不显著.

为了计算F的值，需用到QR和QE的值，下列公式是常用的：

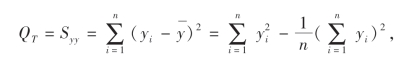
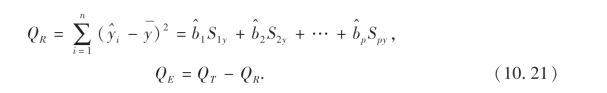
例7 试对例6中线性模型的假设进行检验，α=0.05.

解

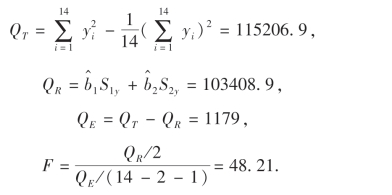
查表得F0.05（2，11）=3.98，故F ＞F0.05（2，11），线性回归显著.