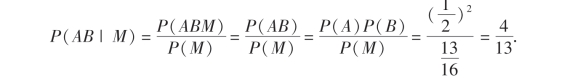多个事件的独立性
下面,我们把两个事件间的相互独立性推广到更多个随机事件的情形.
定义7 如果有限个事件A1,A2,…,An(或可列无限多个事件A1,A2,…,An,…)中的任意两个事件是相互独立的,则称它们是两两相互独立的.
显然,有限个事件A1,A2,…,An两两相互独立应同时满足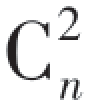 个关系式:
个关系式:
![]()
定义8 如果对n个事件A1,A2,…,An中的任意m 个事件Ai1,Ai2,…,Aim,1≤i1<i2<… <im≤n,2≤m≤n,都满足关系式则称A1,A2,…,An是总体相互独立的,或简称为A1,A2,…,An相互独立.

![]()
注2:如果A1,A2,…,An总体相互独立,则其中的任意m个事件(2≤m≤n)必定总体相互独立.这是由于A1,A2,…,An中的任意m个事件的相互独立性应满足的2m-m-1个等式包含在(1.23)式的2n-n-1个等式之中.

证略.
由定义8和7可知,总体相互独立比两两相互独立有着更高的要求.即当A1,A2,…,An总体相互独立时,它们必定两两相互独立,而其逆不一定成立.例如,设Ω={ω1,ω2,ω3,ω4}是某一古典型随机试验的样本空间.事件A={ω1,ω2},B={ω1,ω3},C={ω1,ω4},则
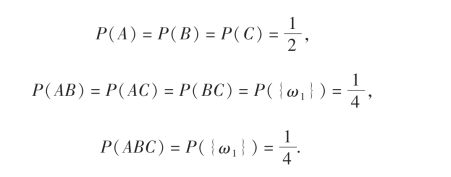
从而
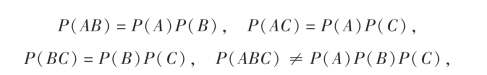
故事件A,B,C是两两相互独立的,但不是总体相互独立.
由定义8可知,若要验证n个事件的相互独立性,需检查(1.23)式中2n-n-1个关系式是否成立,当n较大时其计算量是非常大的,在实际问题中,对于事件的独立性,我们往往不是利用定义来判断,而是根据实际意义来加以判断的.
下面举例说明独立性概念的一些应用.
例26 有3批种子,发芽率分别为0.9,0.8和0.85.在这三批种子中各任取一粒.求取得的3粒种子中至少有一粒能发芽的概率.
解 设A表示事件“取得的3粒种子中至少有一粒能发芽”,Ai表示事件“由第i批中取出的一粒种子能发芽”,i=1,2,3,则事件A1,A2,A3相互独立,且
![]()
由一般加法公式(1.12)得
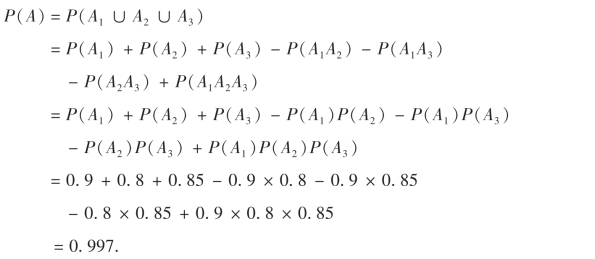
如果我们利用本章第3节的推论1,即公式(1.11)来求P(A),则计算非常简单.
因为
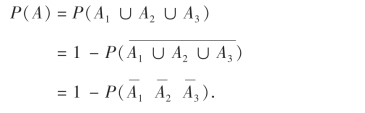

(1)灯亮的概率;
(2)灯亮时,开关a与b同时关闭的概率.
解 设A,B,C,D分别表示开关a,b,c,d关闭这些事件,M表示“灯亮”这一事件,则A,B,C,D相互独立,且
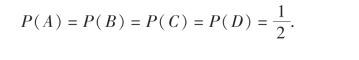
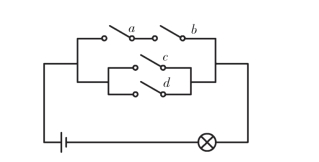
图1-4
(1)M=AB∪C∪D,由一般加法公式,所求概率为
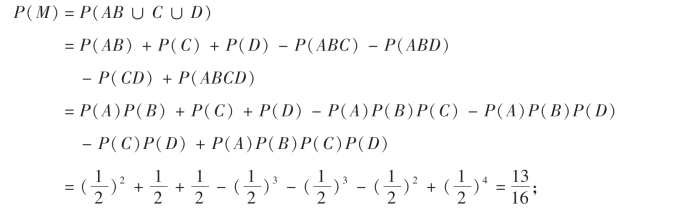
(2)所求概率为P(AB|M),由条件概率的定义并注意到AB⊂M,得到