线性模型假设的检验
上面的讨论是在假设Y与X存在线性回归的条件下求得回归直线方程的.其实,就最小二乘法而言,对任何一组数据(只要xi不全相同)都可用(10.4)及(10.5)给它们配一条直线来描述Y与X间的关系.但在处理实际问题时,μ(x)是否是线性函数,首先要根据有关专业知识做出判断或由实践进行检验.在统计中,人们还可以利用显著性检验来判断,就是说,求得的回归直线方程是否能用来指导实践,一般说来需要经过假设检验来确定.若线性模型的假设符合实际,即Y与X之间确有线性关系,则b不应为零,因为若b=0,Y就不依赖于X或不是线性地依赖X了.因此,首先提出待验假设:
![]()
下面讨论如何进行检验.与方差分析时一样,常用数据总的偏差平方和来衡量数据波动的大小,即
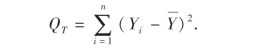
我们把总偏差平方和分解为两部分,一部分是线性关系引起的偏差平方和,另一部分是其余一切因素引起的偏差平方和.为此,令
![]()
它是在X=xi处的一个预测值,有
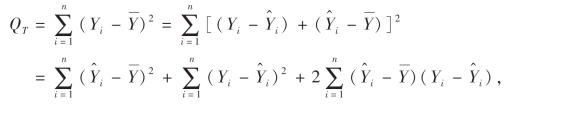
因为
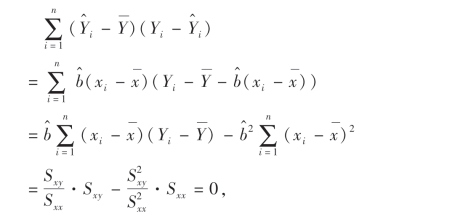
故得
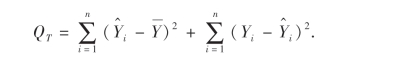
引入记号:
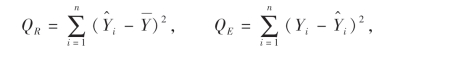
则
![]()
注意到
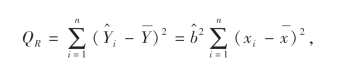
可以看出QR是回归直线上的点由于其横坐标的变化引起的偏差的平方和,即是线性关系引起的偏差平方和,称为回归平方和.而QE则是除去线性因素以外其他因素引起的偏差平方和,称为剩余平方和.
对于一组确定的观测值(xi,yi)(i=1,2,…,n),QT是一个定值.若QR较大,则QE就小,这表示X对Y的线性关系起作用较大,随机因素等起作用较小.反之,随机因素等其他因素起作用较大.
在(10.2)的假定条件下,如果假设H0为真,可以证明统计量
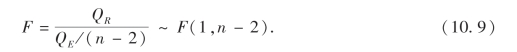
这样,就可用此作为检验统计量,对给定的显著性水平α,当
![]()
时,拒绝假设H0(即否定b=0),而认为Y与X之间确有线性关系,或者说回归效果是显著的,否则认为回归效果不显著.回归效果不显著的原因可能有如下几种:
(1)影响Y取值的除X外,还有其他不可忽视的因素;
(2)Y与X的关系不是线性关系,而存在着其他的关系;
(3)Y的取值与X无关,即Y与X不存在关系.
因此需要进一步分析原因,分别处理.
在具体计算时,除在建立回归方程时,已经计算出的Sxx,Sxy外,还需计算Syy(即QT),QR,QE,及F的值,计算公式为
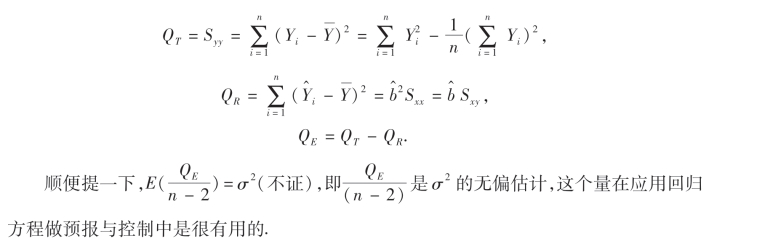
例3 对例2中求得的回归直线方程的显著性进行检验(α=0.05).
解 首先计算出Sxx,Sxy,Syy,这里n=9.
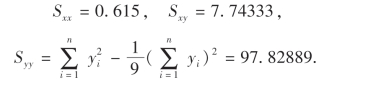
然后计算QT,QR及QE.
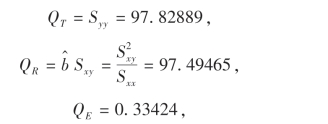
所以
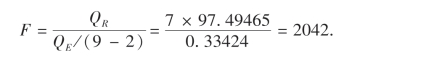
查表得,F0.05(1,7)=5.59,由于F=2042≫5.59,故X对Y的回归方程效果非常显著,所建立的回归方程有实用价值.
