§3.3 随机变量的相互独立性
在一般情况下,二维随机变量(X,Y)的性质不能完全由单个随机变量X与Y的性质来确定,因为(X,Y)的性质中考虑了X与Y之间的联系.如果X与Y不存在联系,情况又怎么样呢?为了研究这一问题,我们引入定义5.
定义5 设X与Y为两个随机变量,并设F(x,y),FX(x),FY(y)分别是二维随机变量(X,Y)的分布函数及边缘分布函数.若对所有的x,y有
![]()
则称随机变量X与Y是相互独立的.
以下我们将不加证明地给出(X,Y)是离散型随机变量和连续型随机变量时相互独立的充要条件,这些充要条件在判断随机变量相互独立时较为方便.
(1)离散型随机变量X与Y相互独立的充要条件是对于(X,Y)的所有可能取值(xi,yj),有
![]()
即
![]()
(2)连续型随机变量X与Y相互独立的充要条件是在f(x,y),fX(x),fY(y)的任意公共连续点(x,y)处有
![]()
其中f(x,y),fX(x),fY(y)分别为(X,Y)概率密度及边缘概率密度.
依照上述结论,在例7中,对于二维正态随机变量(X,Y),X与Y相互独立的充要条件是ρ=0.
例8 设二维随机变量(X,Y)的分布律为
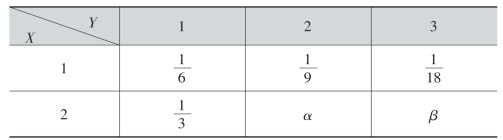
若X与Y相互独立,求α,β之值.
解 由独立性条件有
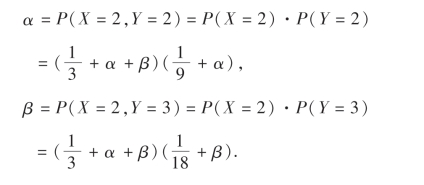
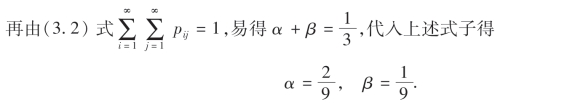
例9 设X与Y是两个相互独立的随机变量,X在(0,0.2)上服从均匀分布,Y的概率密度为
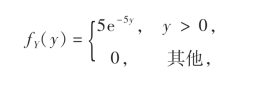
求P(Y≤X).
解 由已知条件得
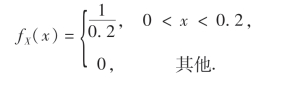
X与Y相互独立,故(X,Y)的概率密度为
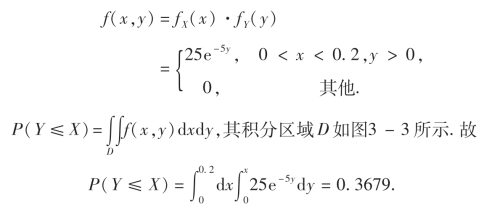
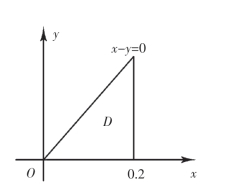
图3-3
以上所述关于二维随机变量的联合分布函数、联合概率密度及独立性等概念,容易推广到n维随机变量中去.
设(X1,X2,…,Xn)为n维随机变量,x1,x2,…,xn为任意实数,则n元函数
F(x1,x2,…,xn)=P(X1≤x1,X2≤x2,…,Xn≤xn)称为(X1,X2,…,Xn)的联合分布函数.
设F(x1,x2,…,xn)为n维随机变量(X1,X2,…,Xn)的联合分布函数,若存在非负函数f(x1,x2,…,xn)使对任意实数x1,x2,…,xn有
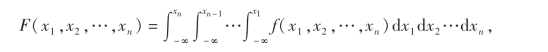
则称(X1,X2,…,Xn)为连续型随机变量,f(x1,x2,…,xn)为n维随机变量的联合概率密度.
设F(x1,x2,…,xn)为n维随机变量(X1,X2,…,Xn)的联合分布函数,FX1(x1),FX2(x2),…,FXn(xn)依次为X1,X2,…,Xn的分布函数,若对任意实数x1,x2,…,xn有
![]()
则称X1,X2,…,Xn是相互独立.
对于n维离散型随机变量的分布律以及独立性,读者可自行给出.
