独立试验概型(贝努里概型)
在实际问题中,常常需要将一个随机试验重复进行若干次(比如n次),如果各次试验的结果互不影响,即每次试验结果出现的概率不受其他各次试验结果的影响,则称这n次试验为n次重复独立试验.
例如,n次掷硬币试验,n次有放回摸球试验,等等,都是n次重复独立试验的简单例子.
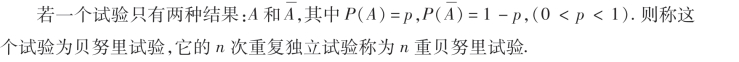
贝努里试验是一种很重要的数学模型,应用非常广泛,有些试验的结果虽然不止两个,但如果我们只注意某一事件发生与否,则也可以化为贝努里试验.例如,在电报传输中,既要传送字母A,B,…,Z,又要传送其他符号,但是假如我们所关心的只是字母在传送中所占的百分比,而不再区别到底是哪一个字母,则我们可以把出现字母当作是“成功”,出现其他符号一律当作“失败”,这时就可以把问题看作是贝努里试验了.
定理9 在n重贝努里试验中,事件A恰好发生k次的概率为
![]()

同时有于是得到
![]()
即(1.25)式右端第一项等于pk(1-p)n-k,同理可得(1.25)式右端其他各项也等于pk(1-p)n-k.所以
![]()
由二项式定理
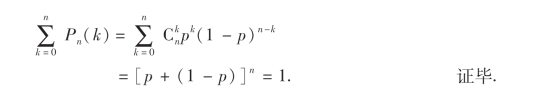
例28 甲、乙两人各掷均匀硬币n次,求两人掷出正面的次数相等的概率.

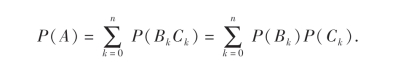
甲掷硬币n次,是n重贝努里试验.由于在每次试验中,掷出正面的概率为![]() ,根据定理9,
,根据定理9,
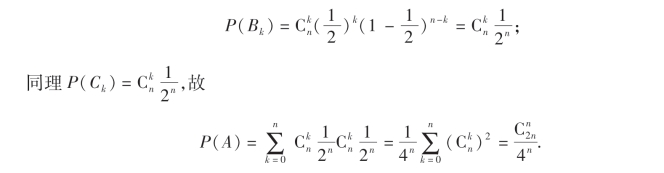
例29 现有一批同类设备,各台的工作是相互独立的,在一段时间内发生故障的概率都是0.01,假定这段时间内一名维修工只能修理一台.
(1)现由一名维修工负责维修这类设备20台,求设备发生故障时不能及时得到维修的概率;
(2)如果由3名维修工共同负责维修这类设备80台,求设备发生故障时不能及时得到维修的概率.
解 (1)把考察每台设备是否需要维修看成一次试验,A表示事件“该台设备需要维修”.考察20台设备发生故障的情况,相当于20次独立重复试验.“设备发生故障时不能及时得到维修”相当于“在20次独立重复试验中,事件A至少发生2次”.
由于P(A)=0.01,故所求概率为
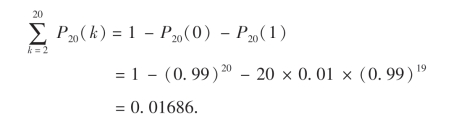
(2)同理,有80台设备时,可以看成80次独立重复试验.在由3名维修工共同负责其维修工作时,“设备发生故障不能及时得到维修”相当于“在80次独立重复试验中,事件A至少发生4次”[p=P(A)=0.01].故所求概率为