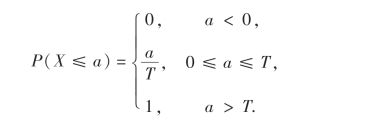随机变量的概念
在随机试验中,我们的观察对象常常是一个或若干个随机取值的量,观察的目的是要了解它们取各可能值或在某个范围内取值的概率.在第一章中我们遇见过许多这样的问题,因此研究随机试验中随机取值的量具有重要意义.
例1 有5件产品,其中2件是次品(用a1,a2表示),3件是正品(用b1,b2,b3表示),任意从中取2件,这个随机试验的样本空间为
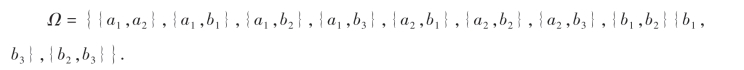
以X表示抽取的两件产品中包含的次品个数,则X是定义在Ω上的一个函数,即X=X(ω),ω∈Ω.具体写出这个函数如下:
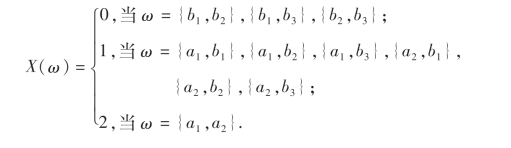
在一次试验中,若出现样本点{a1,b3},则X就取值1,若出现样本点{b2,b3},则X就取值0,一般地,若出现了样本点ω,则X就取对应值X(ω).由于在每次试验中究竟出现哪一个样本点带有随机性,所以X的取值也就带有随机性.
例2 考虑“记录某电话交换台一分钟内接到的呼唤次数”这一随机试验.试验的结果本身就是用数量描述的,以X表示电话交换台一分钟内接到的呼唤次数,则X是一个随机取值的量.X的取值由试验的结果所确定,随着试验的不同结果而取不同的值,因此X是定义在样本空间Ω={0,1,2,3,…}上的函数,即
![]()
有些看起来与数值无关的随机现象,也可以用随机取值的量来描述.
例3 抛一枚硬币,观察正面ω1、反面ω2出现的情况.这一随机试验的样本空间为Ω={ω1,ω2}.每次试验出现的结果为正面或反面,与数值没有关系.现按如下方法引进一个定义在样本空间Ω上的函数X:
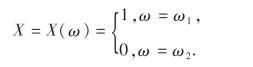
由于试验结果的出现是随机的,因此X(ω)的取值也是随机的.
在以上例子中,各引进了一个随机取值的量X,用它来描述我们所关心的随机现象,这样的量称为随机变量.
定义1 设E是随机试验,它的样本空间为Ω.如果对于每一个ω∈Ω,都有唯一的实数X(ω)与之对应,则称X(ω)为定义在Ω上的一个随机变量,简记为X.
对于随机变量,一方面我们要知道它可能的取值,并用它来表示事件;另一方面我们关心的是它在一定范围内取值的概率.例如,在例1中,事件“取出的两件产品中没有次品”可用{ω:X(ω)=0}表示,事件“取出的两件产品中至少有一件次品”可用{ω:X(ω)≥1}表示,容易求得它们的概率分别为
![]()
例4 在约会问题中(第一章第3节例13),样本空间为
![]()
设X表示甲到达约定地点的时刻,则X为随机变量.试求:对于给定的实数a,事件{X≤a}的概率P(X≤a).
解 X是样本点的函数:X(x,y)=x,(x,y)∈Ω.
当0≤a≤T时,
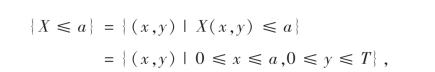
按几何概型
![]()
当a<0时,{X≤a}是不可能事件,从而P(X≤a)=0;
当a>T时,{X≤a}为必然事件,故P(X≤a)=1.
综合即得