§5.2 大数定律
前面提过，我们在引入概率这一概念时，我们利用了随机事件的频率具有稳定性这一特性.事实上，不仅随机事件的频率具有稳定性，很多一般的平均结果也都具有稳定性.这就是说，无论个别随机现象的结果以及它们在进行过程中的个别特征如何，大量随机现象的平均结果实际上与各个个别随机现象的特征无关，并且几乎不再是随机的了.所有这些事实都应该由概率论做出理论上的分析，这也是大数定律需研究的课题.
概率论中用来阐明大量随机现象的平均结果具有稳定性的一系列定理统称为大数定律.
如果在一个n重贝努里试验中，事件A共发生了nA次，则事件A在n次观察中的频率为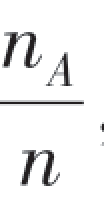
， 设事件A在一次试验中发生的概率为p，我们已经知道，当n增大时，频率逐渐稳定到概率，现在要问，是否有
成立呢？
答案是否定的，因为若成立，我们就可以说“频率以概率为极限”.事实上，上述极限关系若成立，则意味着，对任意ε ＞0，存在充分大的正整数N，对一切n＞N都有
成立.而我们知道，频率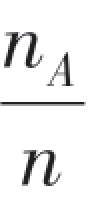
是随着试验结果而改变的，在n重贝努里试验中，下面的试验结果还是有可能发生的：
显然，当n→∞时，pn→0，所以频率靠近概率意味着
其中ε是任意一大于零的常数.这就是下面的贝努里大数定律：
定理1（贝努里大数定律） 设nA是n重贝努里试验中事件A发生的次数，p是事件A在每次试验中发生的概率，则对任意ε＞0，有
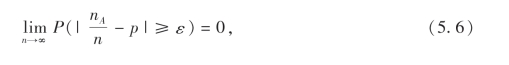
或
则X1，X2，…，Xn是n个相互独立的随机变量，且
E（Xk）=p，D（Xk）=p（1-p）=pq， k=1，2，…，n.
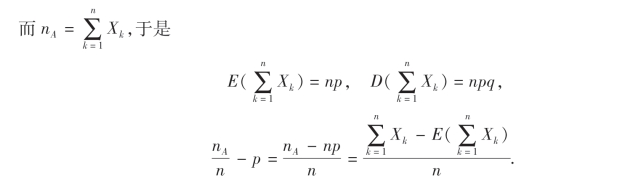
由切比雪夫不等式
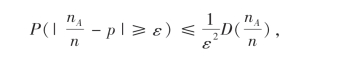
可得
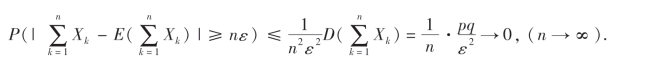
所以
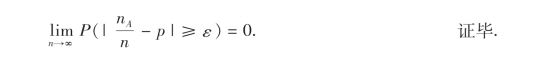
频率的稳定性是可以直接观察到的一种客观现象，而上面的贝努里大数定律则是从理论上给出这种现象更加确切的含义，即当试验次数n足够大时，事件发生的频率与概率有较大偏差的概率很小.因此，在实际应用中，当试验次数n很大时，便可用事件发生的频率近似代替事件发生的概率.由于此类定律说明了大次数的重复试验所呈现的客观规律，这也是称这类定律为大数定律的原因.
从贝努里大数定律的证明过程可以看到，实质上我们讨论了形如
的随机变量在n→∞时的统计规律，其中｛Xk｝，k=1，2，…，n是一系列独立的随机变量.由此得到启发，对于一般意义的一列独立随机变量，我们引入下述更为一般的大数定律——切比雪夫大数定律.
定理2（切比雪夫大数定律） 设X1，X2，…，Xn，… 是相互独立的随机变量，且分别有数学期望E（Xk）和方差D（Xk），（k=1，2，…，n），若方差有界，即存在常数C，使得D（Xk）≤C，则对于任意的ε＞0，恒有
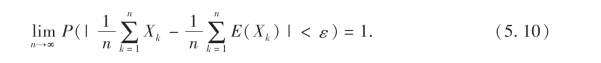
证 因为｛Xk｝，k=1，2，…，n相互独立，故
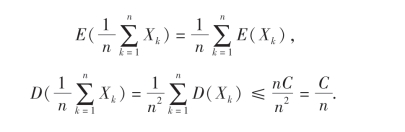
由切比雪夫不等式有
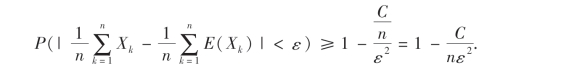
于是，当n→∞时，有（5.10）式成立.证毕
切比雪夫大数定律是贝努里大数定律的推广，而贝努里大数定律是切比雪夫大数定律的一个特例，我们还有下面的推论：
推论 设X1，X2，…，Xn，…是相互独立的随机变量，服从同一分布，并且有数学期望μ和方差σ2，则对于任意的ε＞0，恒有
给出任意的正数ε，如果事件｛|Xn-a|＜ε｝发生的概率当n→∞趋于1，即
推论中要求所讨论的随机变量的方差存在，但实际上，方差存在这个条件并不是必要的，我们有以下定理.
定理3*（辛钦大数定律） 设随机变量X1，X2，…，Xn，… 相互独立，服从同一分布，且有数学期望μ，则对任意的ε＞0，有
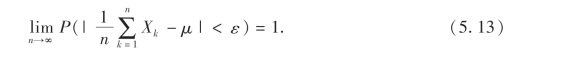
证略.
定理3在度量理论中有特别重要的意义，它是“算术平均法则”的理论依据.比如，我们要测量某一度量μ，在不变的条件下，重复测量n次，得到的观察值x1，x2，…，xn是不完全相同的，这些结果可以看作服从同一分布的n个相互独立的随机变量X1，X2，…，Xn的试验值（它们有数学期望μ），由推论知，当n充分大时，取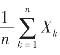
作为μ的近似值所产生
的误差很小.定理3也是后面参数估计中矩估计法的理论基础.