小结

本章是概率论的重点.概率统计是从数量上来研究随机现象统计规律，为了便于数学上的推导和计算，我们把基本事件（样本点）与实数对应产生了随机变量，随机变量的取值与基本事件对应，基本事件是随机的，故随机变量的取值有随机性，试验前只知道它可能的取值范围，而不能预知它取什么值.有了随机变量，使我们能利用数学分析的理论和方法来研究随机试验与随机事件，从而完成对随机试验结果的规律性的研究.

理解离散型随机变量的定义、分布律的概念，理解连续型随机变量的定义和概率密度函数的概念，掌握概率密度函数的性质.离散型随机变量的取值范围是有限集或可列无限集，连续型随机变量是在一个、几个有限区间内或无限区间内连续取值，它取任意一个点的概率为零；离散型随机变量的分布函数F（x）一般是阶梯函数，即F（x）是分段常数，X的取值点xk（k=1，2，…）为F（x）的间断点，P（X=xk）=pk为F（x）相应的跳跃值；连续型随机变量的分布函数必为连续函数，它是一条连续曲线.但是要注意反过来不一定成立.

理解随机变量的分布函数的定义和了解其性质，理解连续型随机变量概率密度函数的概念，掌握概率密度函数的性质.一个随机变量X的分布函数有下面三个性质：（1）F（x）是单调不减函数；（2）0≤F（x）≤1，F（-∞）=0，F（+∞）=1；（3）F（x）是右连续函数.这三个性质是分布函数的充要条件，缺一不可.一个函数f（x）是某一随机变量X的概率密度的充要条件是：（1）f（x）＞0；（2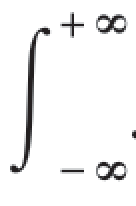）f（x）dx=1，这两个条件缺一不可.

掌握（0-1）分布、二项分布、泊松分布、均匀分布、指数分布、正态分布，特别是正态分布中标准正态分布表、一般正态分布概率计算、正态分布的性质、标准正态分布密度函数的对称性等，它们在实际应用中是非常重要的.正态分布有极其广泛的实际背景.例如，测量的误差、产品的数量指标（直径、长度、体积、重量等）、材料的疲劳应力、粮食的亩产量等，都服从或近似服从正态分布.一个变量如果受到大量微小的、独立的随机因素的影响，那么，这个变量一般是一个正态分布.另一方面，有些分布（如将在第六章介绍的χ2分布、t分布等）又可通过正态分布导出，有些分布（如二项分布、泊松分布等）的极限分布是正态分布.所以，正态分布是概率论中最重要的分布.

随机变量函数Y=g（X）的分布是用来解决由已知随机变量的分布去求出另一个与之有关随机变量分布的问题.掌握求随机变量函数的概率分布的基本方法，一般地，由y=g（x）决定Y的取值范围，但在离散型变量的情形要注意相同值的合并.正确计算Y的分布，当y=g（x）单调变化时，可直接代公式求解；如果y=g（x）不是单调的，用分布函数法求解：先求Y的分布函数FY（y），再求导得fY（y）.