三、t分布

三、t分布

定义5 设X ～N（0，1），Y～χ2（n），且X与Y独立，则称随机变量

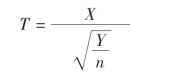
服从自由度为n的t分布，记作T～t（n）.

例2 设随机变量X和Y相互独立且都服从正态分布N（0，32），而X1，X2，…，X9和Y1，Y2，…，Y9分别是来自总体X和Y的简单随机样本，问统计量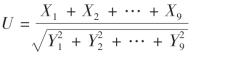服从什么分布？参数是多少？

解 由已知得Xi～N（0，32），（i=1，2，…，9），且X1，X2，…，X9相互独立，故

于是

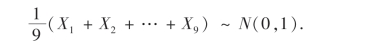
又由Y～N（0，32）得

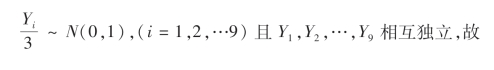
于是

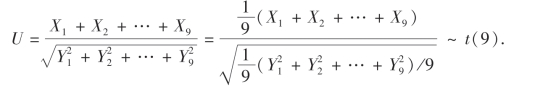
设T～t（n），则T的概率密度函数为

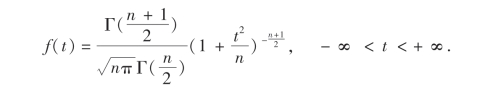
t分布的概率密度函数f（t）的图形关于纵轴t=0对称.当n充分大时，其图形近似于标准正态分布的随机变量的概率密度函数的图形，但对于较小的n，t分布与N（0，1）分布相差很大（图6-4）.

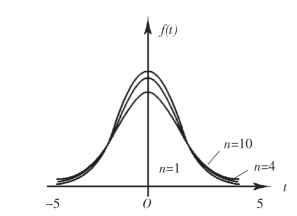
图6-4

t分布的分位点：设T ～t（n），T的概率密度函数为f（t），对于给定的正数α，0＜α ＜1称满足条件

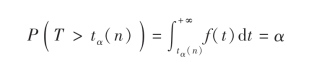
的点tα（n）为t分布的上α分位点.

由t分布的上α分位点定义及t分布的概率密度函数图形的对称性知

t分布的上α分位点可从附表四查得.在n＞45时，可用标准正态分布的上α分位点来近似：