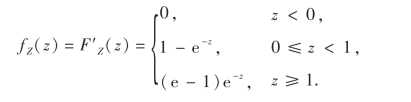Z=X+Y的分布

一、Z=X+Y的分布

我们分两种情况讨论：

设（X，Y）是二维离散型随机变量，其分布律为P（X=xi，Y=yj）=pij，i，j=1，2，…，则Z=X+Y也是离散型随机变量，且Z的一切可能的取值zk是X的可能取值xi与Y的可能取值yj的和，即

但由于对不同的xi及yj，它们的和xi+yj可能是相等的，所以由概率的有限可加性或可列可加性得

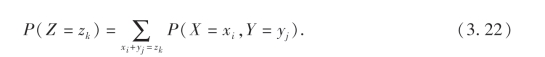
这里的求和范围是一切使xi+yj=zk的xi及yj的值.特别地，如果X和Y是相互独立的，则有

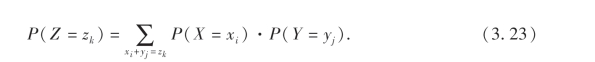
例12 设（X，Y）的分布律为

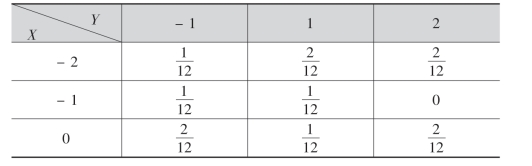
试求Z=X+Y的分布律.

解 从（X，Y）的分布律可得

由此得Z=X+Y的分布律

设（X，Y）是二维连续型随机变量，其概率密度为f（x，y），则Z=X+Y的分布函数为

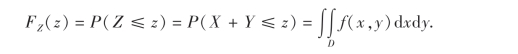
其中积分区域D是位于直线x+y=z左下方的半平面（图3-4），化为二次积分得

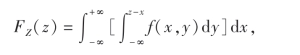
令y=v-x，并交换积分次序得

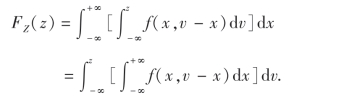
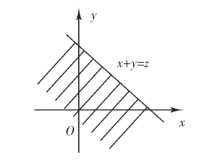
图3-4

可见，Z也是连续型随机变量，其概率密度为

由X与Y的对称性，fZ（z）又可写成

如果X与Y相互独立，则（3.24）及（3.25）式可写成

和

例13 设X和Y是相互独立的随机变量，且都服从标准正态分布N（0，1），试求Z=X+Y的概率密度.

解 由题意

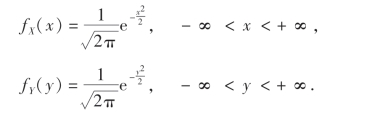
因为X和Y相互独立，由（3.26）式有

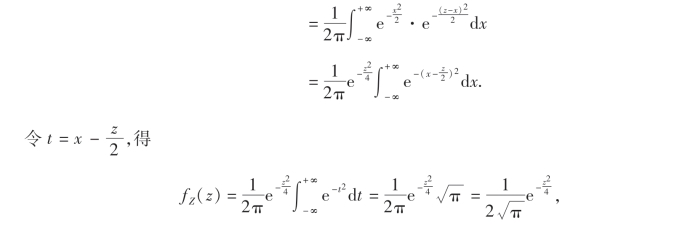
即Z服从N（0，2）分布.

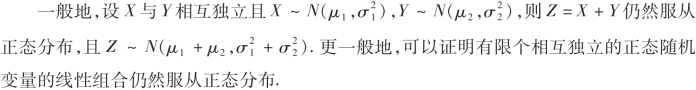
例14 设X和Y是两个相互独立的随机变量，其概率密度分别为

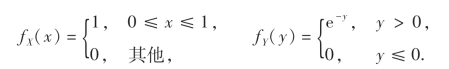
试求Z=X+Y的概率密度.

解 因X和Y相互独立，得

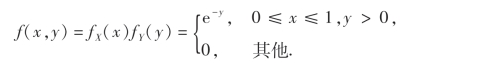
Z=X+Y的分布函数为

以下就z的取值分三种情况讨论：

（1）当z＜0时，显然FZ（z）=0.

（2）当0≤z＜1时，由图3-5可知

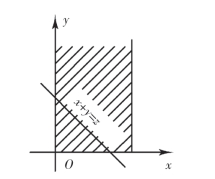
图3-5

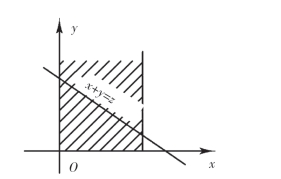
图3-6

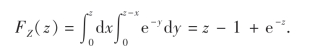
（3）当z≥1时，由图3-6可知

故Z=X+Y的概率密度为