二维离散型随机变量

二、二维离散型随机变量

定义3 如果二维随机变量（X，Y）的所有可能的取值是有限对或可列无限多对，则称（X，Y）是二维离散型随机变量.

设二维离散型随机变量（X，Y）所有可能的取值为（xi，yj），i，j=1，2，…，称P（X=xi，Y=yj）=pij为二维离散型随机变量（X，Y）的概率分布或分布律，或称为随机变量X与Y的联合分布律.

（X，Y）的联合分布律如下表所示：

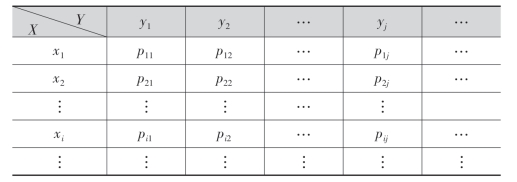
由概率的定义，（X，Y）的联合分布律具有以下性质：

知道了二维离散型随机变量（X，Y）的分布律，可求得（X，Y）的分布函数F（x，y）为

其中求和是对所有满足xi≤x，yj≤y的点（xi，yj）进行.

例1 设随机变量X在1，2，3，4四个整数中等可能地取值，另一个随机变量Y在1～X中等可能地取一整数值，求（X，Y）的分布律.

解 X的可能取值为1，2，3，4，Y取不大于X的正整数，因此

当i＜j时，pij=P（X=i，Y=j）=0；

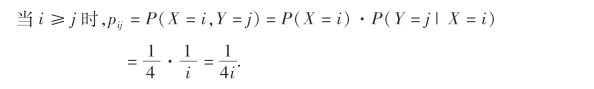
所以，（X，Y）的分布律为

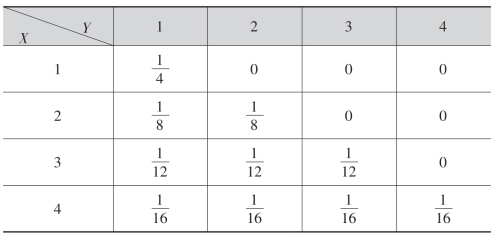
例2 设随机变量（X，Y）的分布律为

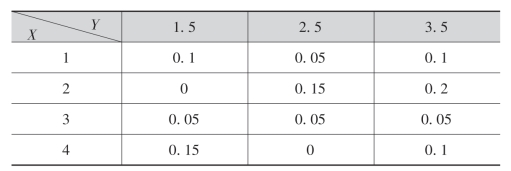
求P（|X-Y|=0.5）.

解 满足条件|X-Y|=0.5的（X，Y）的所有可能取的值为：（1，1.5），（2，1.5），（2，2.5），（3，2.5），（3，3.5），（4，3.5），因此所求概率即为（X，Y）在这些点上取值的概率之和.即