四、相关系数

四、相关系数

在实际应用中，常用相关系数来检验线性模型的假设.上段我们已经获得

规定

即R的大小反映出回归平方和在总偏差平方和中所占的比例，从而反映了Y与X线性关系的密切程度.显然0≤R≤1.特别地，当QR=QT即QE=0时，R=1（线性关系最密切）；当QR=0时，R=0（线性关系最不密切）；反之亦成立.另外，

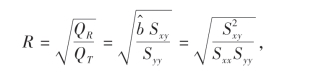
由这一公式可见，当把X看成随机变量时，它就是X与Y的样本相关系数.所以这里也把R叫作相关系数.

为了利用R进行检验，注意到它与F之间的关系：

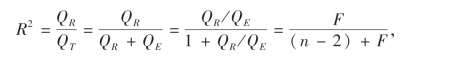
由F的临界值Fα（1，n-2），由上式算出R的临界值Rα（n-2）（n-2称为R的自由度），这个临界值对给定的显著水平及自由度已经列表附在书后以备查用.

综上所述，若R＞Rα（n-2），则否定假设b=0，而认为Y与X确有线性关系；否则认为线性关系不显著.

现用相关系数对例2中求得的回归直线方程的显著性进行检验.由例3知

所以

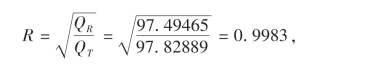
查表得R0.05（7）=0.666，故R＞R0.05（7），且R非常接近1，从而认为回归方程效果极显著，即认为Y与X之间存在线性关系.