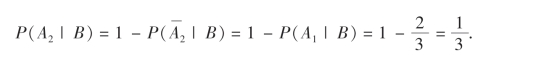条件概率的定义及性质
在实际问题中,除了要考虑事件A的概率P(A)外,常常还需要考虑在事件B已发生的条件下,事件A发生的概率.由于增加了新的条件“事件B已发生”,所以这时A发生的概率与P(A)不一定相同.为了区别,我们把它称为在“事件B已发生”的条件下,事件A发生的条件概率,记为P(A|B).
例17 将一枚均匀的硬币掷两次,观察正反面出现情况.设A为事件“正、反面各出现一次”,B为事件“至少掷出一次正面”,求P(A)和P(A|B).
解 这是一个古典概型,样本空间为Ω={(正,正),(正,反),(反,正),(反,反)},A={(正,反),(反,正)},故
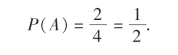
下面求P(A|B).
如果知道事件B已经发生,那么试验所有可能的结果组成的集合就是B={(正,正),(正,反),(反,正)},B中含有3个样本点,其中有2个样本点属于A.于是,在“事件B已发生”的条件下,事件A发生的条件概率为
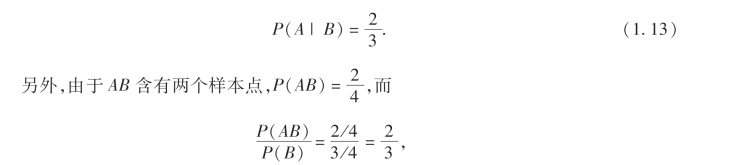
所以(1.13)式可以写成
![]()
对于古典概型,(1.14)式是有普遍意义的,事实上,设样本空间Ω含有n个样本点,A,B是两个事件,B和AB所含的样本点个数分别为m和k.在事件B已经发生的条件下,试验一切可能的结果为B中的样本点,这时A发生当且仅当AB中的某一样本点发生,故
![]()
对于几何概率和统计概率也有相同的结果,因此,我们将关系式(1.14)作为条件概率的一般定义.
定义5 设A,B是两个事件,且P(B)>0,称

为在“事件B已发生”的条件下,事件A发生的条件概率.
定理2 设P(B)>0,则条件概率P(·|B)满足概率的公理化定义中的三个条件,即
(i)非负性,对任一事件A,有
![]()
(ii)规范性:
![]()
(iii)可列可加性:对可列无限多个互不相容的事件A1,A2,…,An,…有
![]()
证明略.
既然条件概率满足概率定义的三个条件,故定理1及其推论中所得到的概率的性质,全适用于条件概率P(·|B).例如,对于任意事件A1,A2有
![]()
例18 袋中有2m-1个白球和2m个红球,随机地从中一次取出m个球,发现都是同一种颜色的,求这颜色是红色的概率和是白色的概率.
解 设A1为事件“取出的m个球全是红色的”,A2为事件“取出的m个球全是白色的”,B为事件“取出的m个球是同一颜色”,则
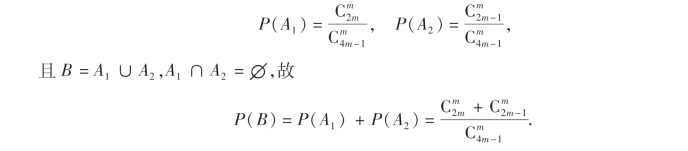
由条件概率的定义并注意到A1B=A1,可知在取得的m个球是同一颜色的条件下球全是红色的条件概率为

因为在B已发生的条件下,A1与A2互为对立事件,故在取得的m个球是同一颜色的条件下,球全是白色的条件概率为