两个正态总体方差比的F检验

二、两个正态总体方差比的F检验

我们在用T检验法检验两个总体的均值是否相等时，做了一个重要的假设，就是这两个总体方差是相等的，即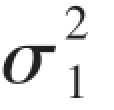==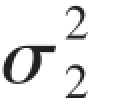σ2，否则我们就不能用T检验.如果我们事先不知道方差是否相等，就必须先进行方差是否相等的检验.

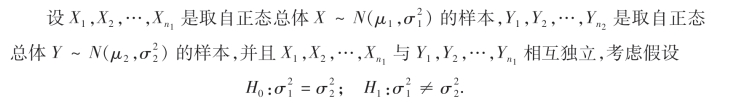
（1）当总体的期望μ1，μ2均已知时：

（2）当总体的期望μ1，μ2均未知时：

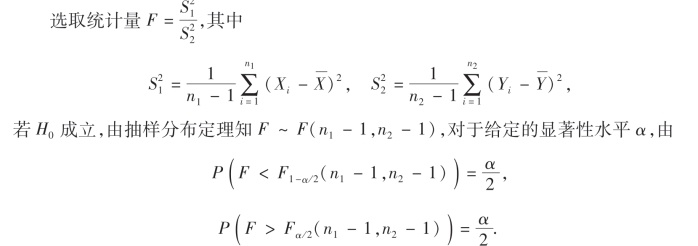
则此时的拒绝域为

这种使用的统计量服从F分布的检验法称为F检验法.

注：（1）在查F分布表时，只有右侧临界值，因此，实际计算F时，就恒有F＞1，当给定显著水平α后，查表得Fα/2，这样只需F ＞Fα/2或F≤Fα/2便可判断接受或拒绝H0.

（2）两个正态总体方差的单侧检验的拒绝域在第194页的表格中给出.

例11 某种烟叶在进行处理前后各抽取样本，测得含水率（%）如下：

处理前：19 18 21 30 66 42 8 12 30 27

处理后：15 13 7 24 19 4 8 20若烟叶含水率服从正态分布，问处理前后烟叶含水率的标准差有无显著变化（α=0.05）？

解 根据题意提出假设：

例12 甲、乙两个工厂生产同一种零件，抽取甲、乙两厂零件进行比较，测得重量如下，假定零件重量（单位：千克）服从正态分布，问乙厂零件重量的方差是否比甲厂零件重量的方差小（α=0.05）？

甲厂：93.3 92.1 94.7 90.1 95.6 90.0， 94.7

乙厂：95.6 94.9 96.2 95.1 95.8 96.3

解 由题意提出假设

此题中均值未知，构造统计量

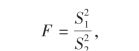
查表求得临界值

而由样本观察值求得的实际值为

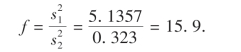
通过比较有f＞Fα（n1-1，n2-1），所以拒绝H0，认为乙厂零件重量的方差比甲厂零件重量的方差小.