一、数学模型

一、数学模型

设随机变量Y与X有相关关系，就是说当X取一确定值时，随机变量Y有一个确定的分布.这个分布大多数情况下不能具体知道，但在实践中只需要知道Y的观测值.而数学期望（假设存在）在一定程度上能反映出其观测值的大小，所以人们感兴趣的是当X取确定值x时，Y的数学期望μ（x）是多少.我们称μ（x）为Y对X的回归函数.

在实际问题中，回归函数是未知的，需要我们根据实测样本以及以往的经验来确定回归函数的类型及求出函数中的未知参数的估计，得到经验公式.

例1 20℃时在铜线含碳量X%对于电阻Y（为一正态变量，单位：微欧）变化的研究中，得到如下一批数据：

测试结果表明，随着铜线含碳量的增加，其电阻有增大的趋势.为了确定回归函数μ（x）的类型，我们将这九组数据作为坐标在平面直角坐标系中描出它们相应的点，这种图称为散点图（图10-1）.可以看出，所有散点大体上散布在一条直线的周围.因此估计μ（x）大致具有线性函数a+bx的形式，即可认为X与Y具有如下关系：

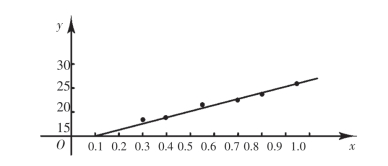
图10-1

其中a，b及σ2是常数.

对n根铜线进行独立观测，能得到n个含碳量x1，x2，…，xn及对应的Y1，Y2，…，Yn，把Yi看作随机变量可以表示成

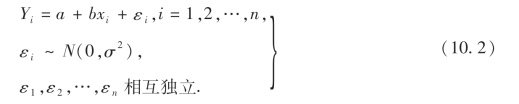
一般地，若随机变量Y与可控变量X满足关系式（10.1），则称Y与X之间存在线性相关关系.进行n次独立随机试验就得到（10.2），我们称（10.1）或（10.2）为一元正态线性回归模型，简称为一元线性模型.

在一元线性回归中主要解决下列问题：

（1）对未知参数a，b及σ2进行估计；

（2）对线性模型的假设进行检验；

（3）对Y进行预测与控制.