*非正态总体的区间估计

四、 *非正态总体的区间估计

实际中经常遇到的一批产品的次品率的估计，就是常见的一种非正态总体的区间估计问题.在这批产品中随机地抽取一个产品，只有两种可能，或者是正品，或者是次品，它可以看成一个服从（0-1）分布的随机变量X，其分布律为f（x，p）=px（1-p）1-x，x=0，1，其中p是未知参数.现设有一容量为n（n＞50）的大样本来自（0-1）分布总体，求p的置信度为1-α的置信区间.

已经知道（0-1）分布的均值和方差分别为

因为样本容量较大，由中心极限定理知

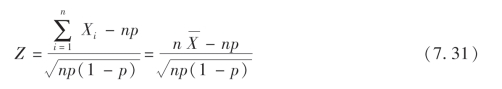
近似服从N（0，1），所以就有

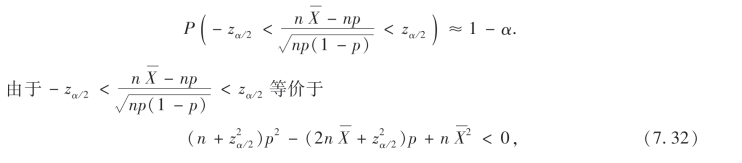
设

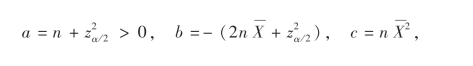
则得

解之得

其中

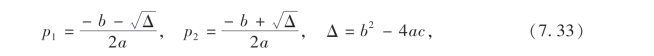
即得p的一个近似置信度为1-α的置信区间为（p1，p2）.

例21 在一批货物的容量为100的样本中，经检查发现有16个次品，试求这批货物次品率p的置信度为95%的置信区间.

解 在这里1-α=0.95，所以α=0.05，α/2=0.025，z0.025=1.96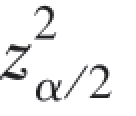，=3.84，n=100，x¯=0.16，由计算公式

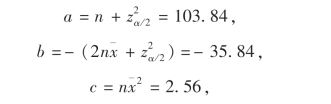
得

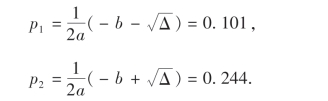
所以，p的置信度为95%的置信区间为（0.101，0.244）.