两个正态总体X ～N（μ1，），Y～N（μ2，）的区间估计

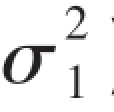三、两个正态总体X ～N（μ 1， ），Y～N（μ 2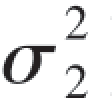， ）的区间估计

在实际工作中常遇到下面的问题：已知产品的某一质量指标服从正态分布，但由于原料、设备条件、操作人员不同，或工艺过程的改变等因素，引起总体均值、总体方差有所改变.我们需要知道这些变化有多大，这就需要考虑两个正态总体的均值差或方差比的估计问题，并做出必要的判断.

设已给定置信度为1-α，并设X，Y是相互独立的正态总体，并设X1，X2，…，Xn1是来自第一个总体的样本（容量为n1），Y1，Y2，…，Yn2是来自第二个总体的样本（容量为n2），且设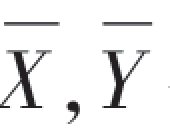分别为第一、二个总体的样本均值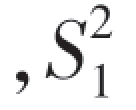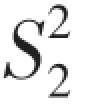，分别是第一、二个总体的样本方差.

1.两个总体均值差μ1-μ2的置信区间

因此，μ1-μ2的置信度为1-α的一个置信区间由下式确定：

求得μ1-μ2的置信度为1-α的置信区间为

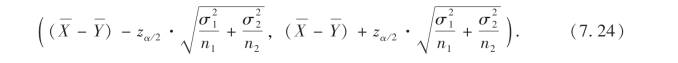
例18 设从总体X ～N（μ1，52）得到一个容量为15的样本，其样本平均值为¯x=19.8，从总体Y～N（μ2，62）得到一容量为18的样本，其样本平均值¯y=24.0，并且两样本相互独立，求μ1-μ2的置信度为0.95的置信区间.

本题中得到的置信区间的上限小于零，在实际中可以认为μ1比μ2小.

其中

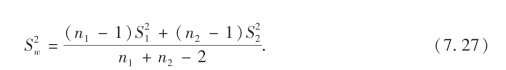
在给定置信度1-α下，应用

可以求得μ1-μ2的置信度为1-α的一个置信区间为

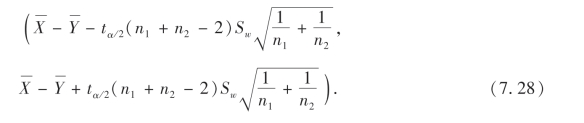
例19 现有A和B两种型号的灯泡，为比较这两种灯泡的使用寿命，随机抽取A型灯泡5只，测得平均寿命为x¯A=1000（小时），样本方差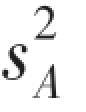=282，随机抽取B型灯泡7只，测得平均寿命¯xB=980（小时），样本方差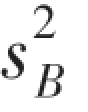=322，假定总体都是正态的，并且由生产过程知它们的方差相等，求两总体均值差μA-μB的99%的置信区间.

解 由于两样本相互独立，两总体方差相等，但未知.在这里1-α=0.99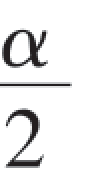，=0.005，n1+n2-2=10.查表知

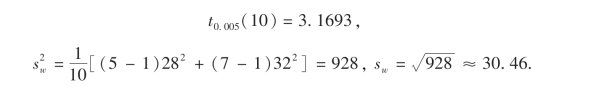
代入（7.28）得μA-μB的置信度为99%的一个置信区间为（-36.5，76.5）.

两总体均值差的置信区间的含意是：若μ1-μ2的置信下限大于零，则可认为μ1＞μ2，若μ1-μ2的置信上限小于零，则可认为μ1＜μ2；若置信区间包含0，可以认为两个总体均值没有显著差别.对于本例就可以认为两个总体均值没有显著差别，不能判定哪个总体均值大.

给定置信度1-α（0＜α ＜1），因为F（n1-1，n2-1）不含任何未知参数，由F分布的上α分位点的定义得

即