多元线性回归中的参数估计

二、多元线性回归中的参数估计

下面用最小二乘法求a，b1，b2，…，bp的估计量.作离差平方和

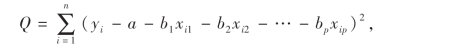
选择a，b1，b2，…，bp，使Q达到最小.由求极值方法，令

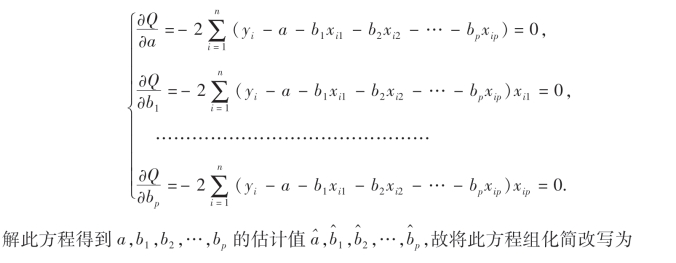
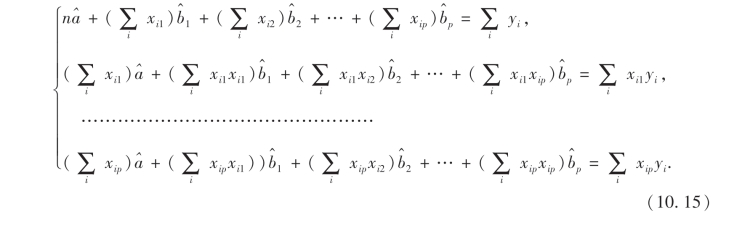
这个方程组称为正规方程（组）.为了把它表示成矩阵形式，记系数矩阵为A，常数项矢量为B，b的估计值矢量为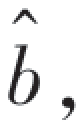则

其中T是表示矩阵转置的记号，于是正规方程（10.15）可表示为下面的矩阵形式

当系数矩阵A=XTX可逆时，可解出

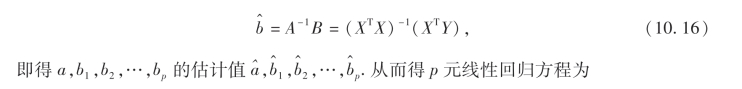
令

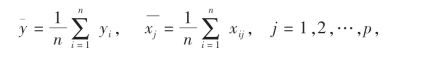
则正规方程（10.15）第一式可变形为

代入（10.17），即得回归方程另一常用形式：

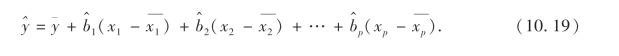
同样，令

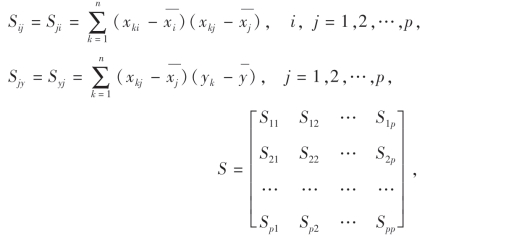
则正规方程（10.15）后p式可以写成

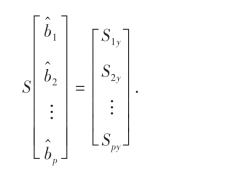
于是我们得到参数估计值的另一求法：

结合（10.18）式即可求得所有参数的估计值.

例6 某铀矿床在勘探坑道内取了14个水样分析水中的铀、钼、镍含量，有关数据列于下表：

试求Y对x1，x2的回归方程.

解 依题意，p=2，n=14.设Y对x1，x2的线性回归方程形式为

所以

于是所求回归方程为