附录 MATLAB中的概率统计
许多同学或学者在学习了概率论与数理统计后,常常有这样一个体会,一个实际问题虽然知道所用的统计方法,但由于实际数据繁多(如近年的全国大学生数学建模竞赛试题),或者计算公式复杂,求出最终结果比较困难,所以对这类问题往往停留在理论探讨上,缺乏具体计算的感性认识和解决实际问题的经验.
如果能结合某种科学计算软件,如MATLAB,MATHEMATICA,SPSS,SAS等科学计算软件,则可方便、迅速、准确地计算出结果,解决实际问题.
本附录只简单介绍MATLAB在概率统计中的若干命令和使用格式,而有关MATLAB的基本知识和程序设计的书籍非常多,在此不做介绍.
1 随机数的产生
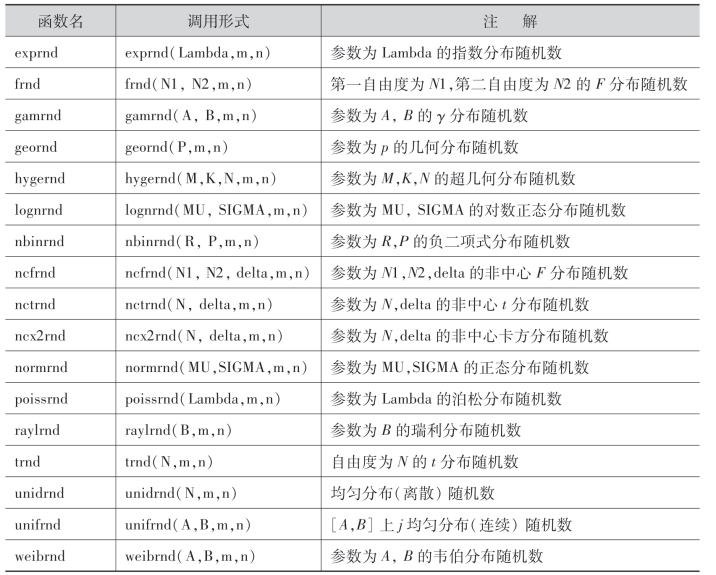
1.1 常见分布的随机数函数
随机数产生函数表

续表
例如:正态分布的随机数据的产生.
命令 参数为μ,σ的正态分布的随机数据

例1.1
n1=normrnd(1:6,1./(1:6))
n1=2.1650 2.3134 3.0250 4.0879 4.8607 6.2827
n2=normrnd(0,1,[15])
n2=0.0591 1.7971 0.2641 0.8717 -1.4462
n3=normrnd([123;456],0.1,2,3)%MU是一个均值矩阵;SIGMA是一个常数,则按MU行列生成一个全为0.1常数矩阵.
n3=0.9299 1.9361 2.9640
4.1246 5.0577 5.9864
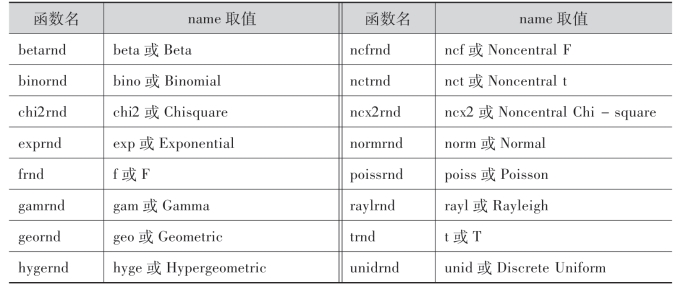
1.2 通用函数求各分布的随机数据

name取值表
续表

命令 求指定分布的随机数例1.2 产生10(2行5列)个均值为0、标准差为1的正态分布随机数.
rn=random(′Normal′,0,1,2,5)
rn=-0.1567 0.2573 1.4151 0.5287 -0.9219
-1.6041 -1.0565 -0.8051 0.2193 -2.1707
例1.3 产生6(1行6列)参数分别为1,2,3,4,5,6的Poisson分布随机数.
rp=random(′Poisson′,1∶6,1,6)
rp=0 0 1 2 5 7
2 随机变量的概率密度计算
2.1 常用分布的概率密度函数值
命令 正态分布的概率值

例2.1 计算标准正态分布在X=-3∶1∶3的值.
Y=normpdf(-3∶1∶3,0,1)
Y=0.0044 0.0540 0.2420 0.3989 0.2420 0.0540 0.0044
例2.2 计算正态分布N(0,1),N(1,2),N(2,2)在X=0的值.
Y=normpdf(0,0∶2,1∶3)% 其中X=0为一个常数,将被扩充为全为0的常数向量.
Y=0.3989 0.1760 0.1065
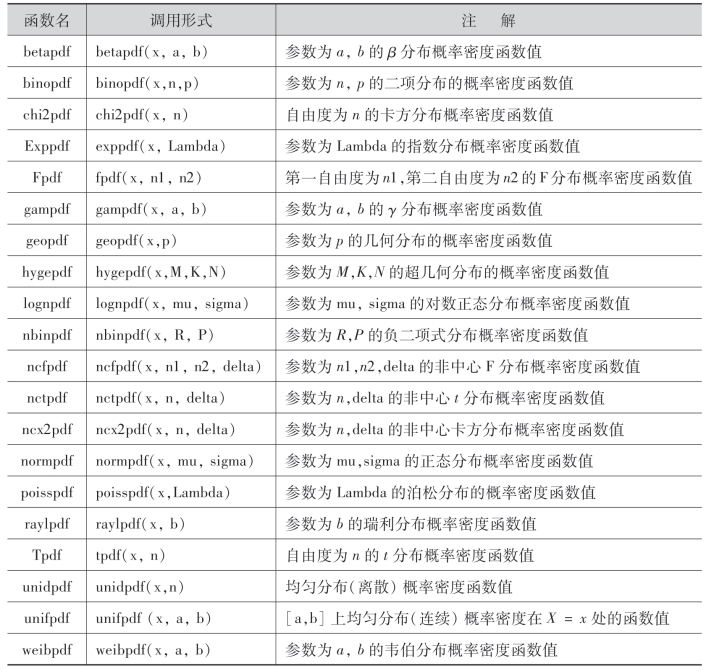
常用概率密度函数列表如下表所示.
常用概率密度函数表
2.2 通用函数计算概率密度函数值
命令 通用函数计算概率密度函数值
函数 pdf
格式 Y=pdf(′name′,X,A)
Y=pdf(′name′,X,A,B)
Y=pdf(′name′,X,A,B,C)
返回在X处,参数为A,B,C的概率密度值,对于不同的分布,参数个数是不同;name为分布函数名,其取值如name取值表所示.
例如,二项分布:设一次试验,事件A发生的概率为p,那么,在n次独立重复试验中,事件A恰好发生K次的概率P—K为:P—K=P{X=K}=pdf(′bino′,K,n,p).
例2.3 计算正态分布N(0,1)的随机变量X=-2∶2时的密度函数值.
解:p=pdf(′Normal′,-2∶2,0,1)
p=0.0540 0.2420 0.3989 0.2420 0.0540
例2.4 绘制卡方分布密度函数在自由度分别为2,6,10的图形.
x=0∶0.2∶30;
y1=chi2pdf(x,2);plot(x,y1,′:′)
holdon
y2=chi2pdf(x,6);plot(x,y2,′+′)
y3=chi2pdf(x,10);plot(x,y3,′o′)
则图形如图1所示.
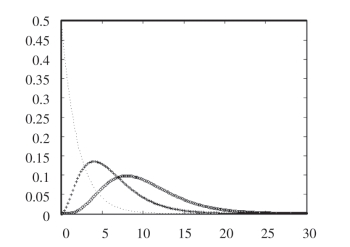
图1
3 随机变量的分布函数值
3.1 常用分布的分布函数值(随机变量的概率之和)
命令 指数分布的分布函数值
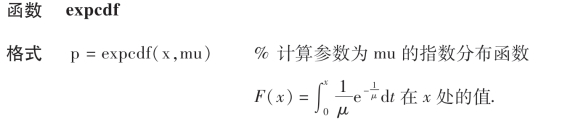
常用分布函数计算累积概率值函数列表如下表所示.
专用函数的累积概率值函数表
3.2 通用函数计算分布函数的值
命令 通用函数cdf用来计算随机变量的概率之和(累积概率值)
函数 cdf
格式 p=cdf(′name′,x,A1)
p=cdf(′name′,x,A1,A2)
p=cdf(′name′,x,A1,A2,A3)
说明 返回以name为分布、随机变量X≤x的概率之和的分布函数值,name的取值见常见分布函数表.
4 随机变量的数字特征
4.1 样本均值和期望
命令 计算样本均值
函数 mean
格式 mean(X) %X为向量,返回X中各元素的平均值.
例4.1 随机抽取6个滚珠测得直径如下(直径:mm):
![]()
试求样本平均值.
解:X=[14.70 15.21 14.90 14.91 15.32 15.32];
mean(X) %计算样本均值
则结果如下:ans=15.0600
命令 由分布律计算数学期望
利用sum函数计算.
例4.2 设随机变量的分布律为

求E(X),E(X2-1).
解:在Matlab编辑器中建立M文件如下:

运行后结果如下:
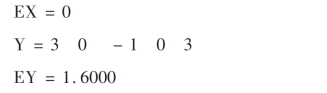
4.2 方差和标准差
命令 求样本方差
函数 var

例4.3 求下列样本的样本方差和样本标准差.
14.70 15.21 14.90 15.32 15.32
解:X=[14.7 15.21 14.9 14.91 15.32 15.32];

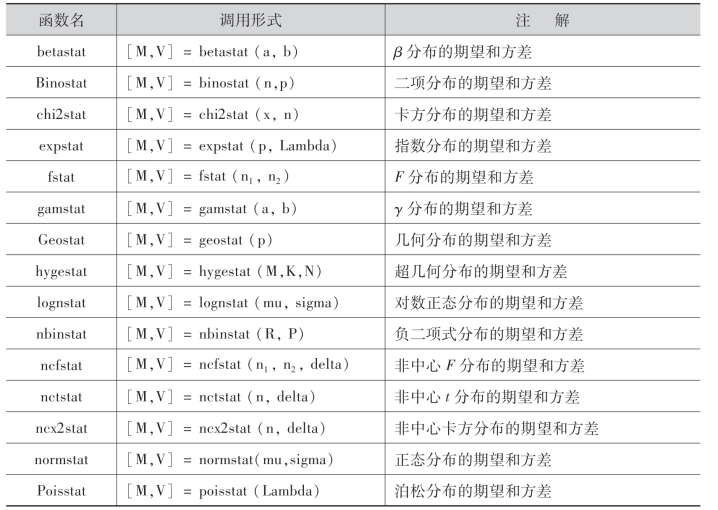
4.3 常见分布的期望和方差
命令 均匀分布(连续)的期望和方差
函数 unifstat
格式 [M,V]=unifstat(A,B) %A,B为标量时,返回值就是区间上均匀分布的期望M和方差V,A,B也可为维数相同的向量或矩阵,则M,V也为相应的向量或矩阵.
例4.4

常见分布的均值和方差
续表
4.4 协方差与相关系数
命令 协方差
函数 cov


例4.6

5 参数估计
5.1 常见分布的参数估计
命令 β分布的参数a和b的最大似然估计值和置信区间
函数 betafit
格式 P=betafit(X) %返回数据向量X的β分布参数a和b的最大似然估计量[P,C]=betafit(X,ALPHA).%P返回数据向量X的β分布参数a和b的最大似然估计量;C返回置信度为(1-ALPHA)×100%参数a和b的置信区间,是一个2×2矩阵,其第1列为参数a的置信下界和上界,第2列为b的置信下界和上界;ALPHA为显著水平.
例5.1 随机产生100个β分布数据,相应的分布参数真值为4和3.则4和3的最大似然估计值和置信度为99%的置信区间为多少?
解:r=betarnd(4,3,100,1);%产生100个β分布的随机数,a=4,b=3.
[p,c]=betafit(r,0.01)%求置信度为99%的置信区间和参数a,b的估计值.
p=3.9010 2.6193
c=2.5244 1.7488 5.2776 3.4898
即估计值3.9010的置信区间是[2.5244,5.2776],估计值2.6193的置信区间是[1.7488,3.4898].
命令 利用mle函数进行参数估计
函数 mle
格式 P=mle(′dist′,X) %返回用dist指定分布的参数最大似然估计值.
[P,C]=mle(′dist′,X) %缺省的置信度为95%.
[P,C]=mle(′dist′,X,alpha) %置信度由alpha确定.
[P,C]=mle(′dist′,X,alpha,pl) %仅用于二项分布,p1为试验次数.
说明 dist为分布函数名(表1.2),如beta(分布)、bino(二项分布)等,X为数据样本,alpha为显著水平,(1-alpha)×100%为置信度.
例5.2
rv=binornd(20,0.75) %产生二项分布的随机数.
rv=16
[p,pci]=mle('binomial',rv,0.05,20) % 求参数的估计值和置信区间,置信度为95%.
p=0.8000
pci=0.5634 0.9427
常用分布的参数估计函数:
参数估计函数表

续表

6 假设检验
6.1 σ2已知,单个正态总体的均值μ的假设检验(U检验法)
函数 ztest
格式 h=ztest(x,m,sigma)
h=ztest(x,m,sigma,alpha)
[h,sig,ci,zval]=ztest(x,m,sigma,alpha,tail)
说明 x为正态总体的样本;m为均值μ0;sigma为标准差;alpha显著性水平,缺省值为0.05;sig为观察值的概率,当sig为小概率时则对原假设提出质疑;ci为真正均值μ的(1-alpha)×100%置信区间;zval为统计量的值.
若h=0,表示在显著性水平alpha下,不能拒绝原假设;若h=1,表示在显著性水平alpha下,可以拒绝原假设.
原假设:H0:μ=μ0=m,
若tail=0,表示备择假设H1:μ≠μ0=m(缺省,双边检验);
tail=1,表示备择假设H1:μ>μ0=m(单边检验);
tail=-1,表示备择假设H1:μ<μ0=m(单边检验).
例6.1 设某电子产品平均寿命5000小时为达到标准,现从一大批产品中抽出12件试验结果如下:

假设该产品的寿命X ~N(μ,1400),试问此批产品是否合格?
解:总体μ和σ已知,该问题是当σ2为已知时,在水平α=0.05下,根据样本值判断μ=5000还是μ≠5000.为此提出假设:
原假设:H0:μ=μ0=5000;
备择假设:H1:μ≠5000;
X=[5059,3897,3631,5050,7474,5077,4545,6279,3532,2773,7419,5116];
[h,sig,ci,zval]=ztest(X,5000,sqrt(1400),0.05,0)
结果显示为
h=0
sig=0.2535
ci=1.0e+003*
4.96655.0088
zval=-1.1418
结果表明h=0,说明在水平下,可接受原假设,即认为此批产品是合格.
假设检验函数表

7 方差分析
7.1 单因素方差分析
单因素方差分析是比较两组或多组数据的均值,它返回原假设—— 均值相等的概率.
函数 anova1
格式 p=anova1(X)
p=anova1(X,group)
p=anova1(X,group,'displayopt')
[p,table]=anova1(...)
[p,table,stats]=anova1(...)
说明 X为一个m×n的输入数据,其各列为彼此相互独立的样本观察值;p为各列均值相等的概率值,若p值接近于0,则原假设受到怀疑,说明至少有一列均值与其余列均值有明显不同.Group是与X对应的分类向量,用来区分向量X中来自不同样本的数据;displayopt=on/off表示显示与隐藏方差分析表图和盒图;table为方差分析表,stats为分析结果的结构;anova1函数产生两个图,分别标准的方差分析表图和盒图.
方差分析表中有6列,第1列(source)显示方差分析表中数据的来源;第2列(SS)显示用于每一列的平方和;第3列(df)显示与每一种来源有关的自由度;第4列(MS)显示是SS/df的比值;第5列(F)显示F统计量的数值,它是MS的比率;第6列显示从F累积分布中得到的概率,当F增加时,p值减少.
例7.1 某灯泡厂用4种不同配料方案制成的灯丝,生产了4批灯泡.在每批灯泡中随机地抽取7个灯泡测其使用寿命(单位:小时),数据列于下表中:试问这四种灯丝生产的灯泡的使用寿命有无显著性的差异?
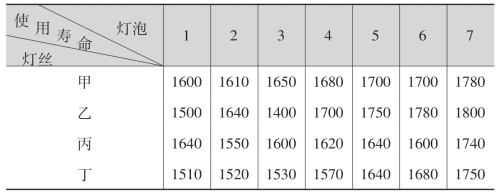

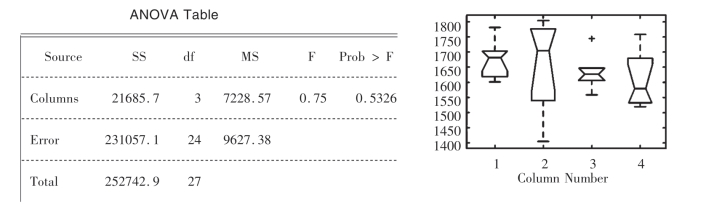
图2
7.2 双因素方差分析
函数 anova2
格式 p=anova2(X,reps)
p=anova2(X,reps,′displayopt′)
[p,table]=anova2(…)
[p,table,stats]=anova2(…)
说明 执行平衡的双因素试验的方差分析来比较X中两个或多个列(行)的均值,不同列的数据表示因素A的差异,不同行的数据表示另一因素B的差异.如果行列对有多于一个的观察点,则变量reps指出每一单元观察点的数目,每一单元包含reps行,如:
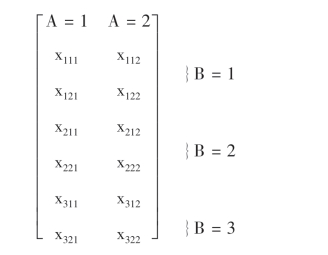
则reps=2.其余参数与单因素方差分析参数相似.
例7.2 某种火箭用4种燃料、3种推进器做射程试验,在试验中,对燃料和推进器的各种水平组合均进行了2次发射试验,射程数据在下表中给出:
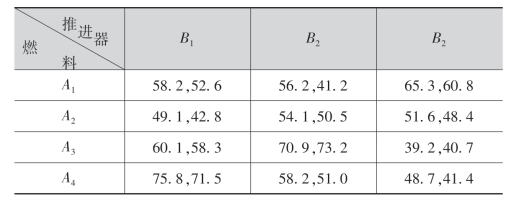
试分析燃料,推进器以及它们的交互作用对射程有无显著性影响.
解:
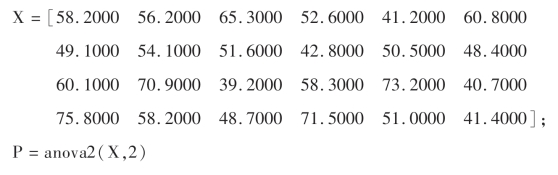
结果为:
P=0.0035 0.0260 0.0001
显示方差分析图为图3.
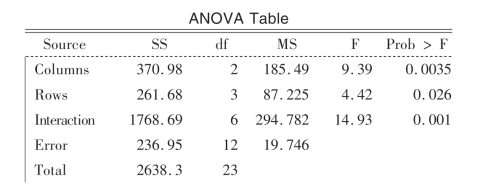
图3
8 回归分析
函数 regress
格式 b=regress(y,X)
[b,bint,r,rint,stats]=regress(y,X)
[b,bint,r,rint,stats]=regress(y,X,alpha)
说明 b=regress(y,X)返回y关于X的最小二乘拟合系数(即回归系数),y是-n×1的列向量,X是-n×p的矩阵,b是-p×1的列向量;bint是b置信度为95%(缺省)的置信区间bint;r是回归残差向量,rint是r的置信度为95%(缺省)的致信区间;stats为回归模型的检验统计量,有3个值,第1个是回归方程的决定系数R2(是相关系数),第2个是统计量值,第3个是与统计量对应的概率值p;alpha为显著性水平.
例8.1 第十章习题第6题.
解:
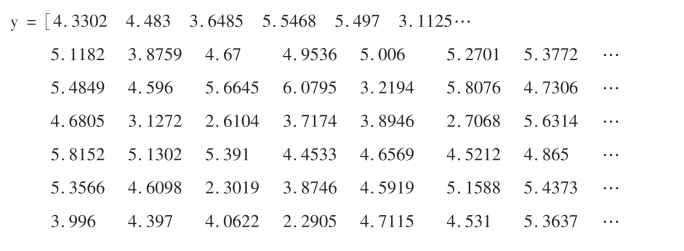


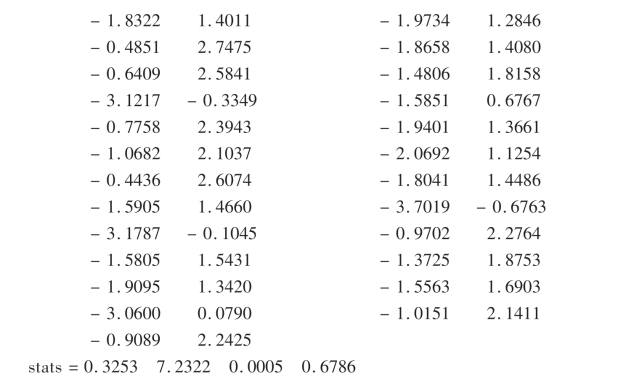
以上简要介绍了MATLAB中的概率统计功能.用于数据处理和统计分析的软件,除MATLAB外,还有MATHEMATICA,SPSS,SAS等.MATHEMATICA纸演算式的数学软件,SPSS(StatisticalPackageforSocialScience)是国际流行的社会科学统计分析软件包,SAS(StatisticalAnalysisSystem)系统是当今国际上公认的功能强大、应用广泛的决策支持系统.
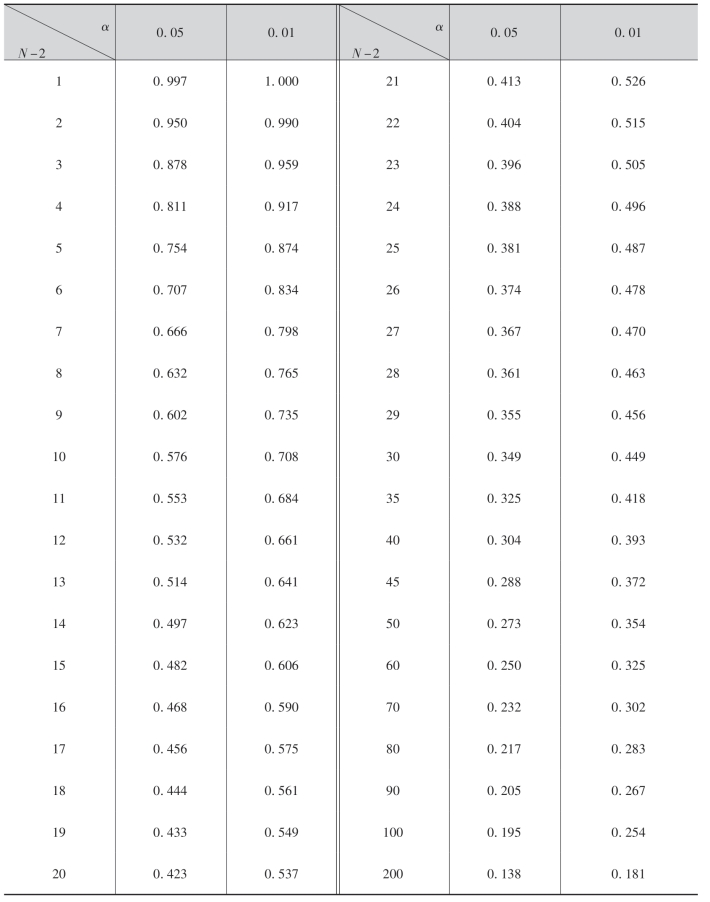
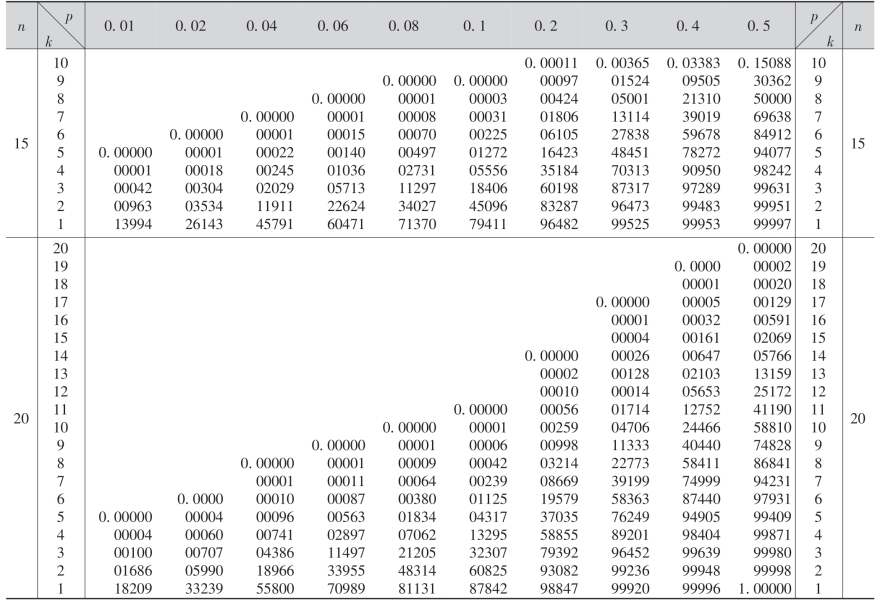
附表一 二项分布表
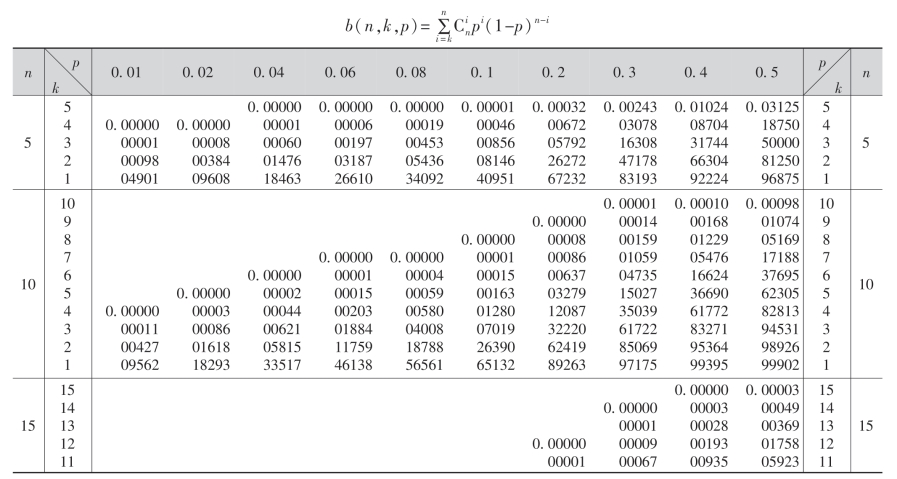
附表一(续)
附表二 标准正态分布表
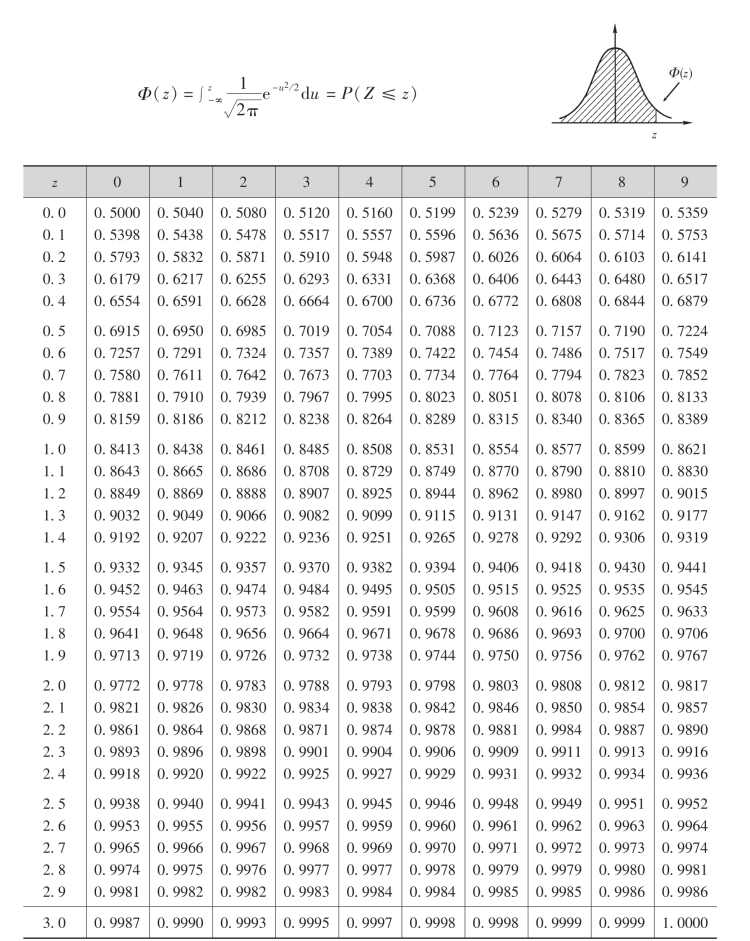
注:表中末行系函数值Φ(3.0),Φ(3.1),…,Φ(3.9)
附表三 泊松分布表
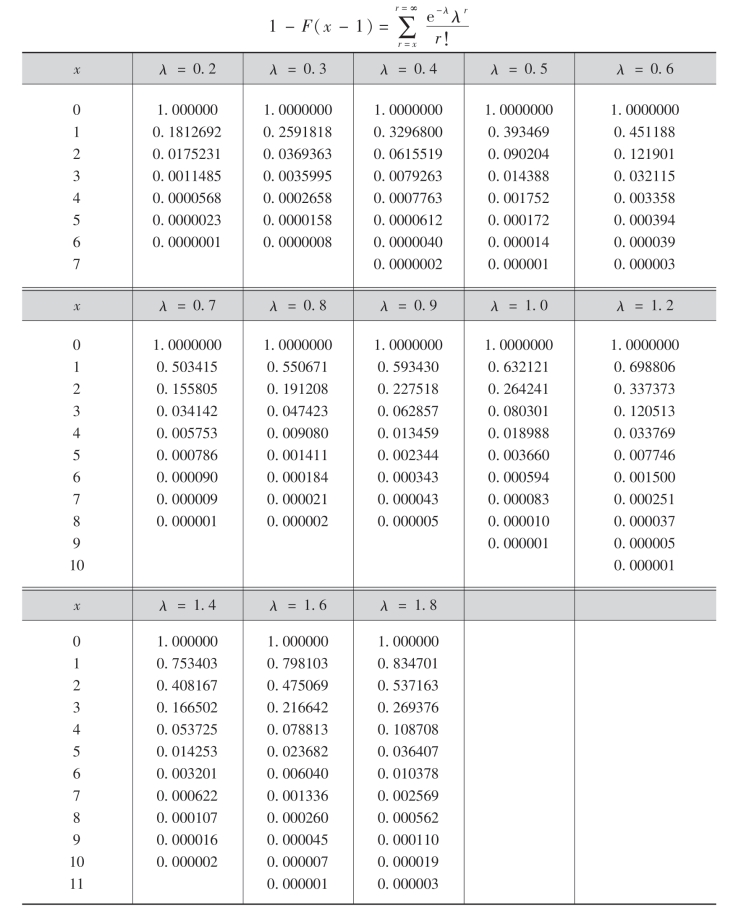
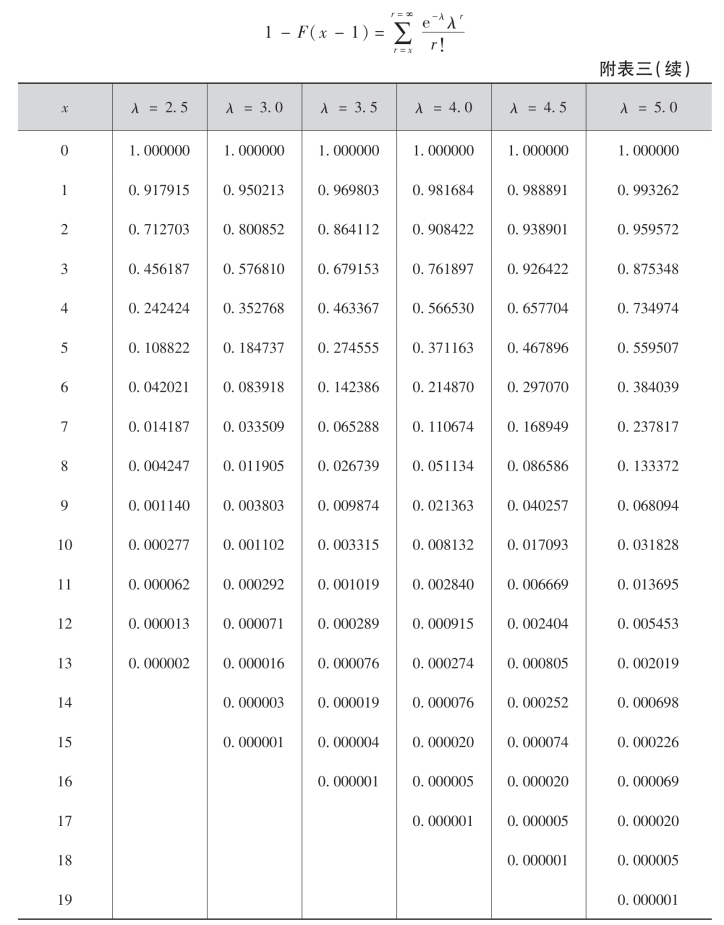
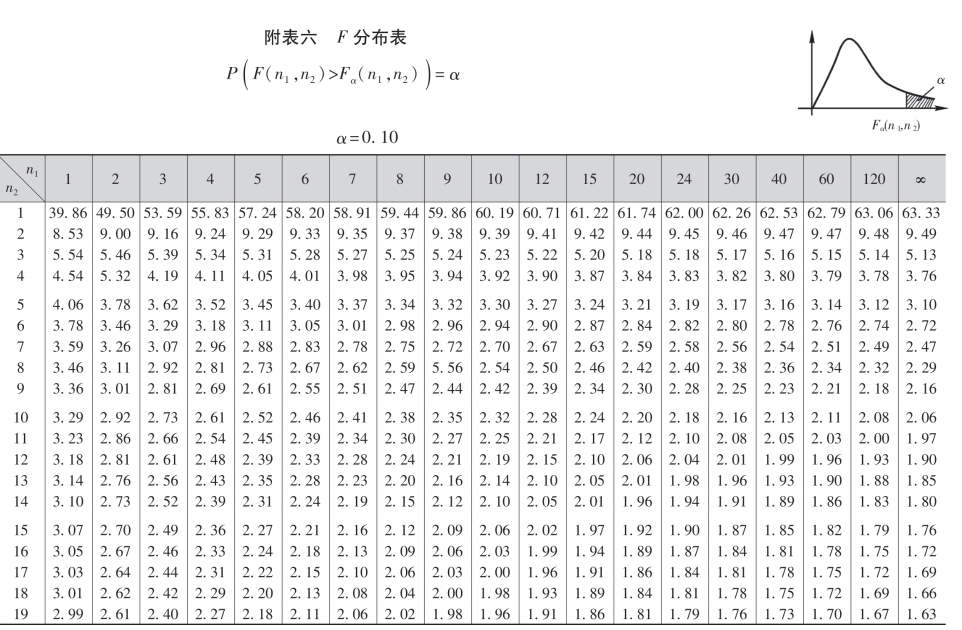
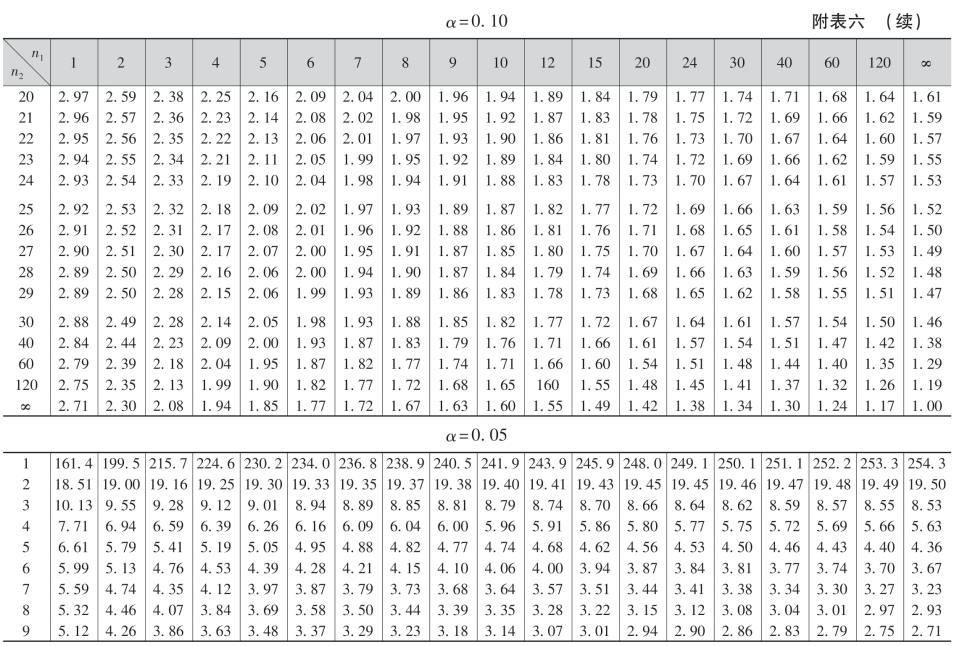
附表四 t分布表
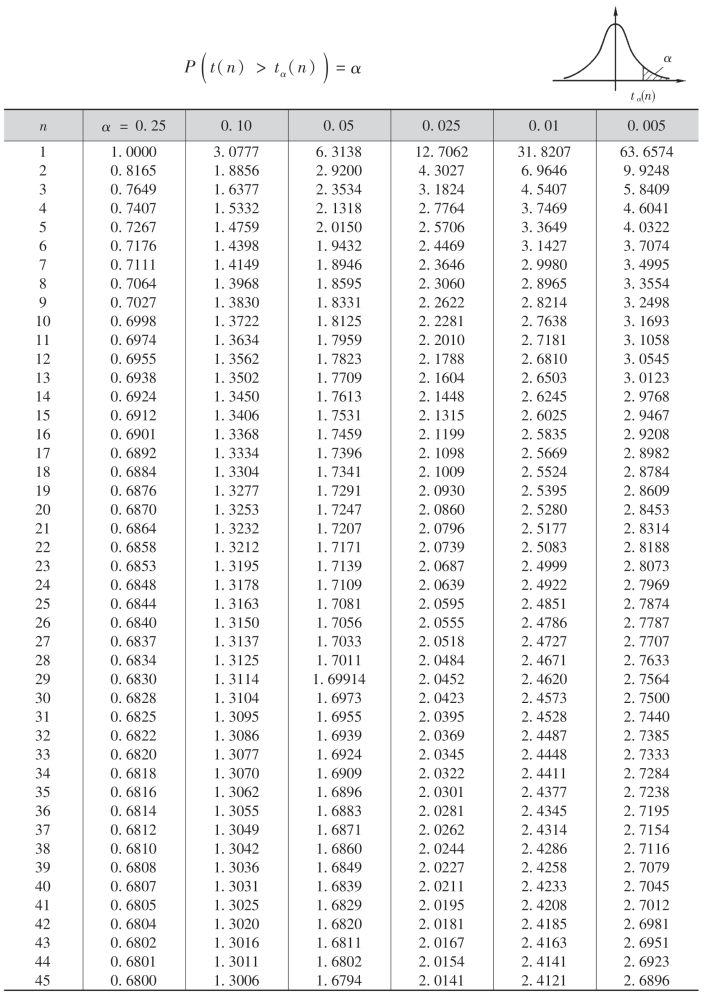
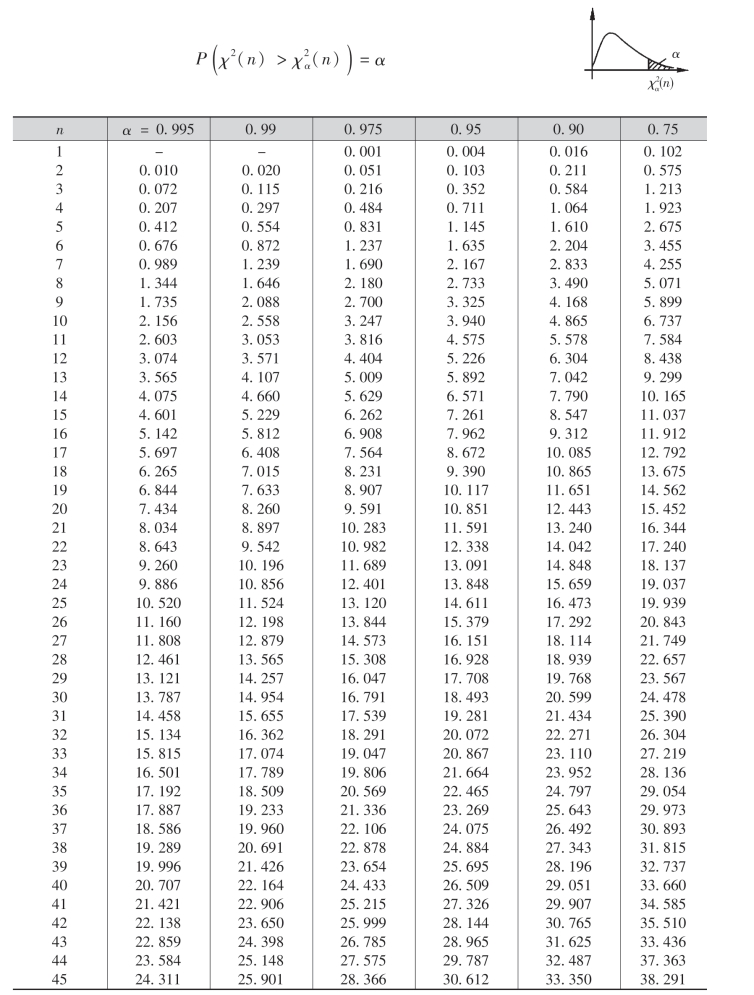
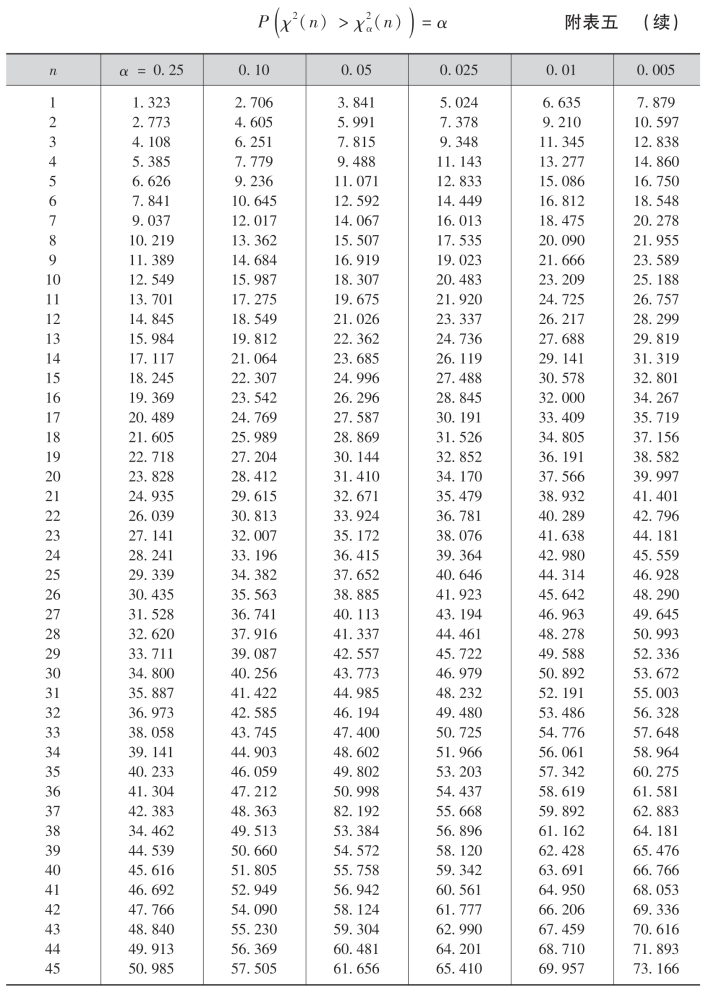
附表五 χ2分布表
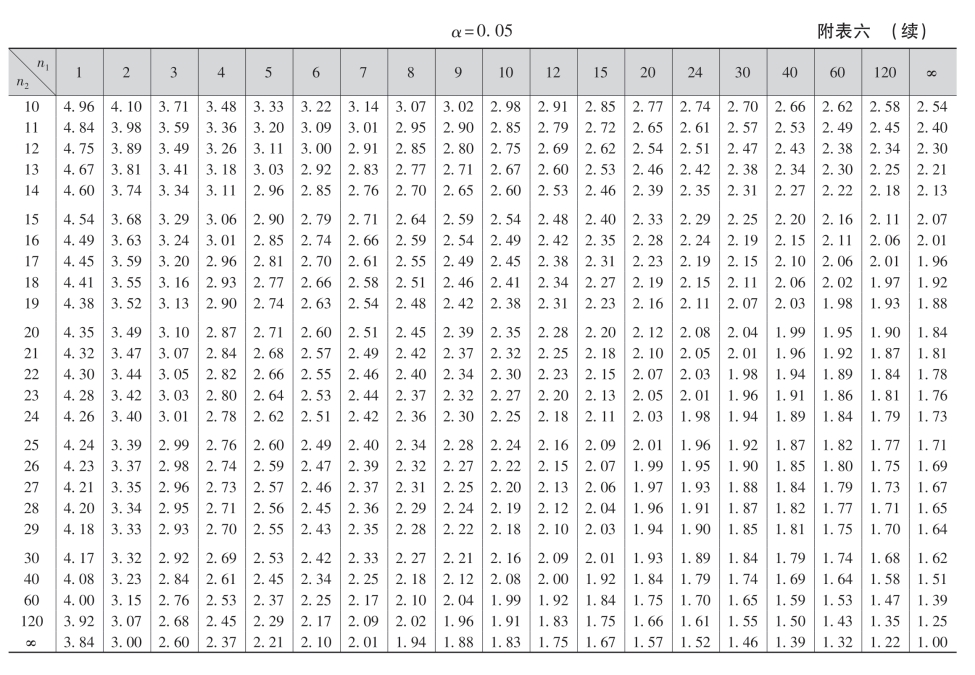
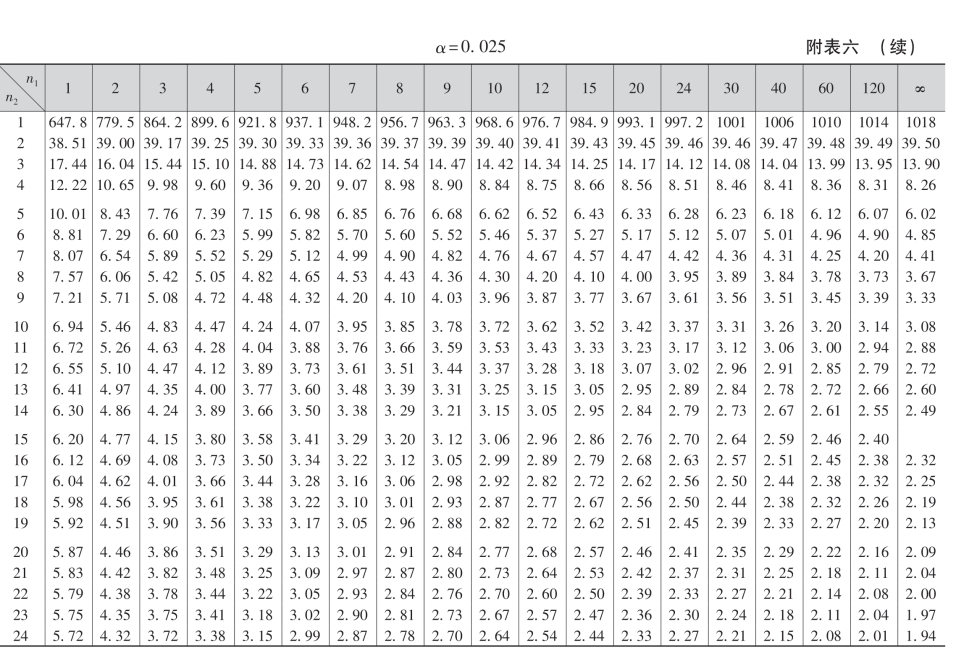
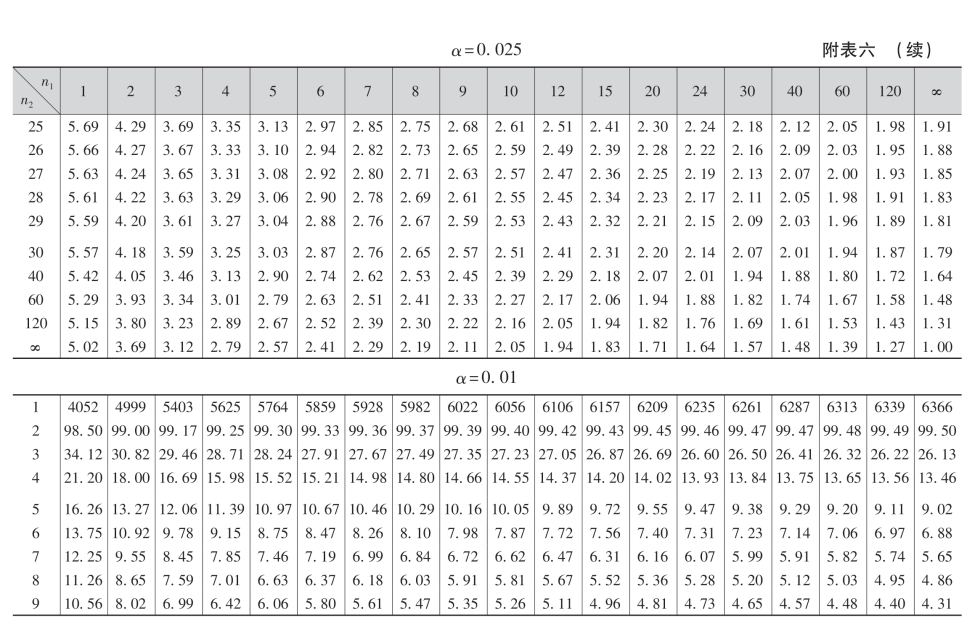
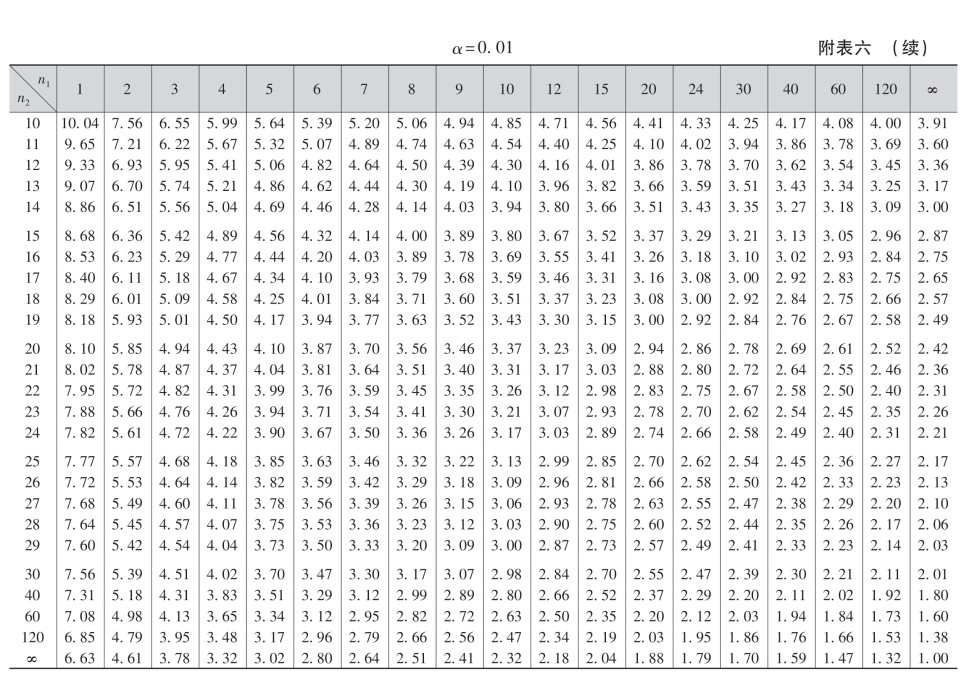
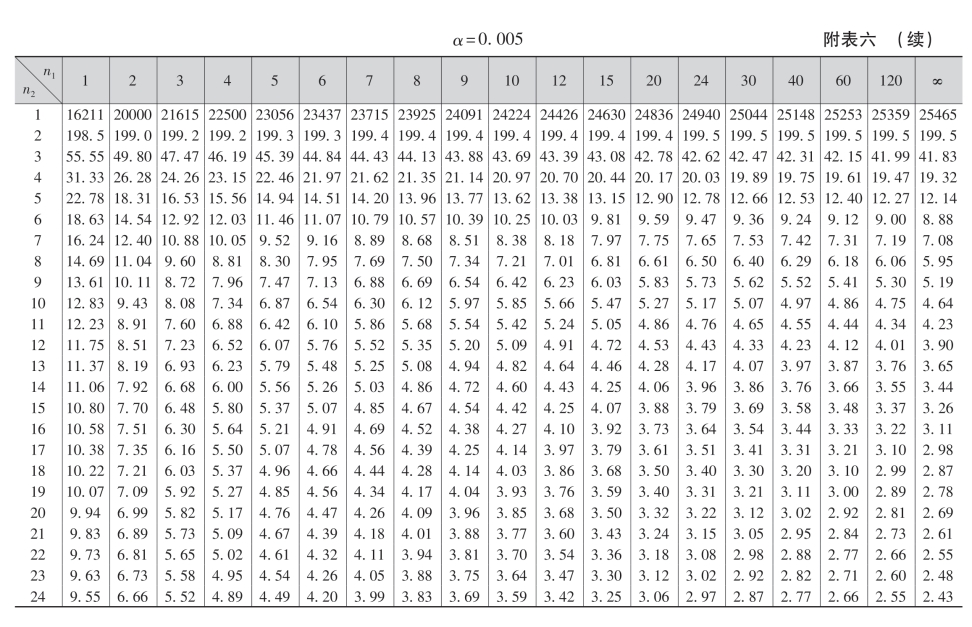
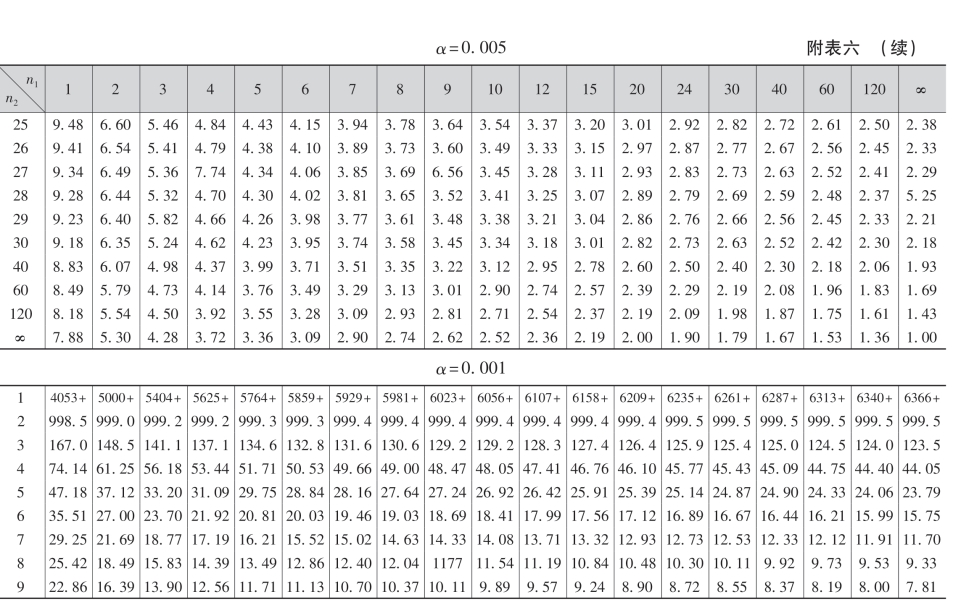
+表示要将所列数乘以100
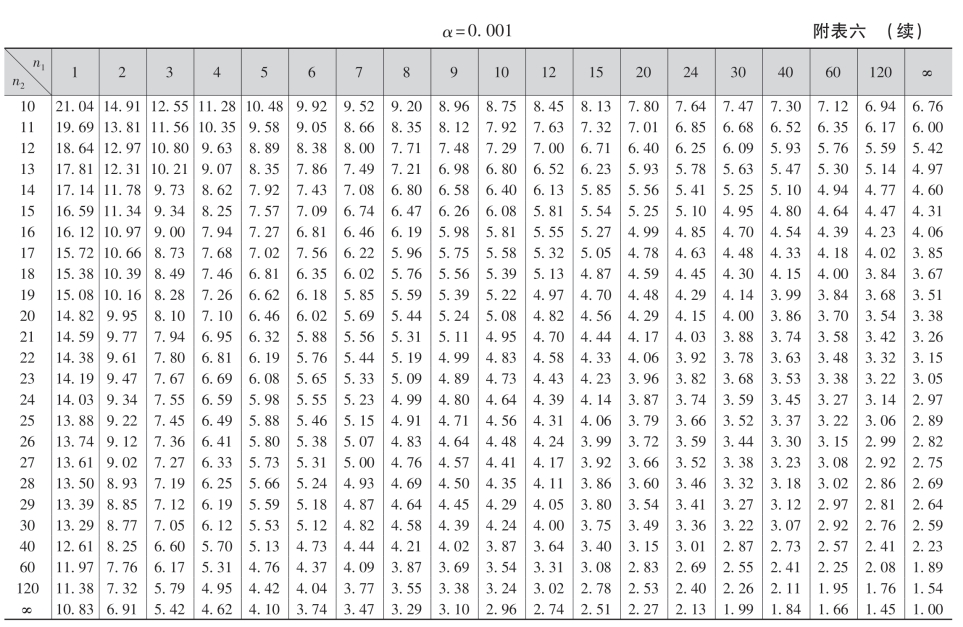
附表七 相关系数检验表