离散型随机变量函数的分布

一、离散型随机变量函数的分布

例17 设离散型随机变量X的分布律为

求Y=3X+2的分布律.

解 由于X分别取值-1，0，1，2时，Y相应的取值互不相同，分别为-1，2，5，8，所以

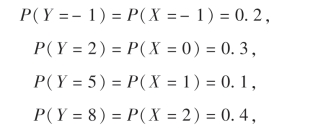
即Y的分布律为

例18 设离散型随机变量X的分布律为

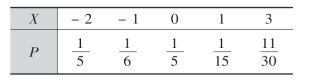
试求Y=X2的分布律.

解 Y所有可能取的值为0，1，4，9.因为

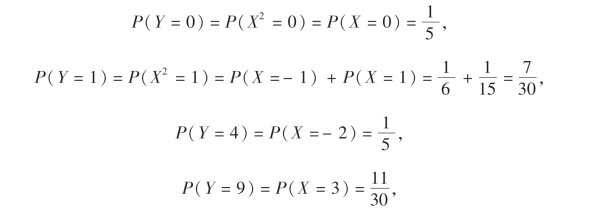
故得Y的分布律为

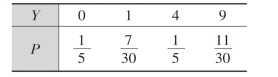
一般，设X是具有下述分布律的离散型随机变量：

而随机变量Y是X的函数，即Y=g（X），则Y也是一个离散型随机变量.当g（x1），g（x2），…，g（xi），…互不相等时，Y具有分布律：

但若某些g（xi）相等时，则Y取该值的概率应是这些g（xi）所对应的pi之和.例如，设a是Y的一个可能的取值，而g（x1），g（x2），…，g（xi），…中至少有两个值等于a，则

其中和式是对于所有满足g（xi）=a的i求和的.