二、χ2检验法
前面介绍了直观而简便的概率图纸法,它不需要很多计算就能对总体分布做出统计推断,并且还能对分布所含的参数做估计.但是这种方法因人而异,且精度不高,又不能控制犯错误的概率.下面介绍皮尔逊提出的χ2检验法,它能够像各种显著性检验一样控制犯第Ⅰ类错误的概率,可用来检验总体是否服从任何一个预先给定的分布.
设总体X的分布未知,根据样本观察值来检验总体分布的假设如下:H0:总体X的分布函数为F0(x);
H1:总体X的分布函数不是F0(x).
在用χ2检验法检验假设H0时,要求在假设H0下F(x)的形式及其参数都是已知的,但实际上参数值往往是未知的,这就需要我们先用极大似然法估计参数,然后再做检验.
χ2检验的基本思想如下:把随机试验结果的全体Ω分为k个互不相容的事件
![]()
于是在假设H0下,我们可以计算pi=P(Ai),i=1,2,…,k.显然,在n次试验中,事件Ai出现的频率ni/n与pi有差异.一般说来,若H0为真,则这种差异并不显著;若H0为假,这种差异就显著.基于这种想法,皮尔逊使用统计量

作为检验假设H0与实际符合程度的尺度,并证明了如下定理:
定理1 若n充分大(n≥50),则不论总体服从什么分布,在H0成立条件下,统计量χ2总是近似地服从自由度为k-r-1的χ2分布.其中,r是被估计参数的个数.
于是,若在假设H0下算统计量χ2有
![]()
则在水平α下拒绝H0;若上式不等号反向,就接受H0.
χ2检验法的具体步骤如下:
设总体的分布函数为F(x),取总体的一个样本X1,X2,…,Xn,现在根据这组样本来检验假设:
![]()
第一步,用极大似然法估计分布中的未知参数.设F0(x)=F0(x,θ1,…,θr),其中θ1,θ2,…,θr为未知参数,利用极大似然法分别求出未知参数θ1,θ2,…,θr的极大似然估计
^θ1,^θ2,…,^θr.
第二步,将实轴分为k个不相交的区间(ai,ai+1],i=1,2,…,k,其中a1=-∞,ak+1=+∞.计算

χ2检验法是在n无限增大时推导出来的,所以在使用时必须注意n要足够大,一般n≥50,同时,要求npi不太小,一般npi≥5;否则,应适当地合并区间,使npi满足要求.
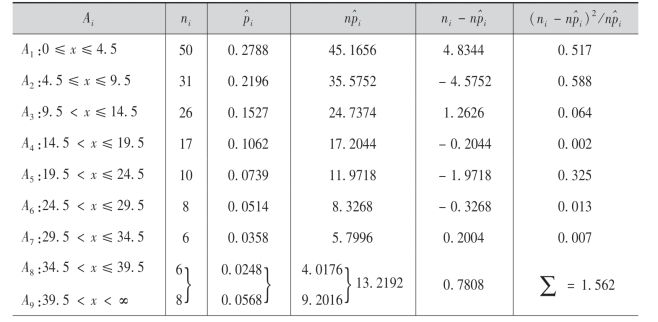
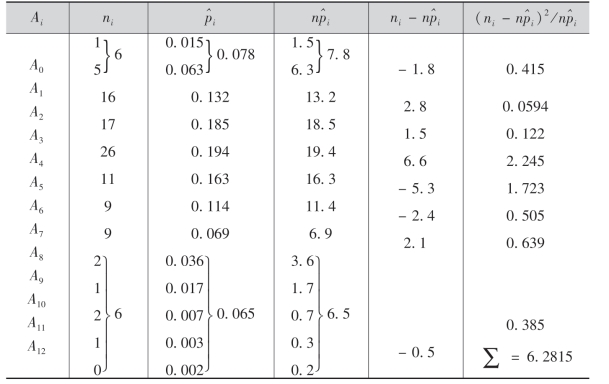
例14 在一实验中,每隔一定时间观察一次由某种铀所放射的到达计数器上的α粒子数X,共观察了100次,得结果如下表所示:

其中ni是观察到有i个α粒子的次数.从理论上考虑知X应服从泊松分布
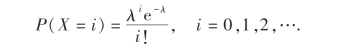
问上式是否符合实际(α=0.05)?即在水平0.05下检验假设
H0:总体X服从泊松分布:
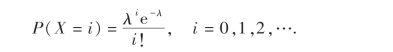
解 因在H0中参数λ未具体给出,所以先估计λ.由极大似然估计得^λ=¯x=4.2.在H0假设下,即在X服从泊松分布的假设下,X所有可能的值为Ω={0,1,2,…},将Ω分成如下表所示的两两不相交的子集A0,A1,A2,A3,A4,A5,A6,A7,A8,A9,A10,A11,A12.则P(X=i)有估计
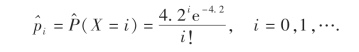
例如:
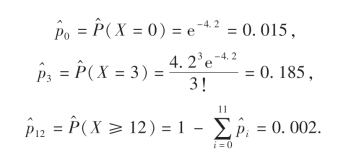

例15 自1965年1月1日至1971年2月9日共2231天中,全世界记录到里氏震级4级和4级以上的地震计162次,统计如下:

试检验相继两次地震间隔的天数X服从指数分布(α=0.05).
解 按题意需检验假设:
H0:X的概率密度为
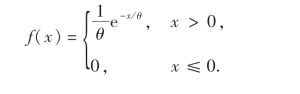

由上式可得概率pi=P(Ai)的估计:
![]()
例如:
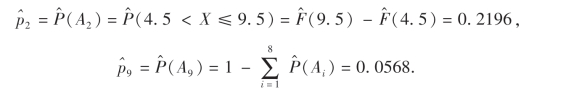
将计算结果列表如下: