两个正态总体均值差的T检验法
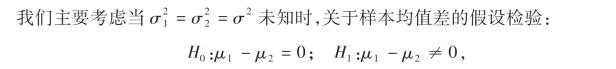
这也等价于
给定显著水平α，当H0成立时
注：（1）关于两个总体均值差的单侧检验的拒绝域在下表中给出.
（2）当两个正态总体的方差为已知时，便可用U检验法来检验两个正态总体均值是否相等的假设，其结果在下表中给出.
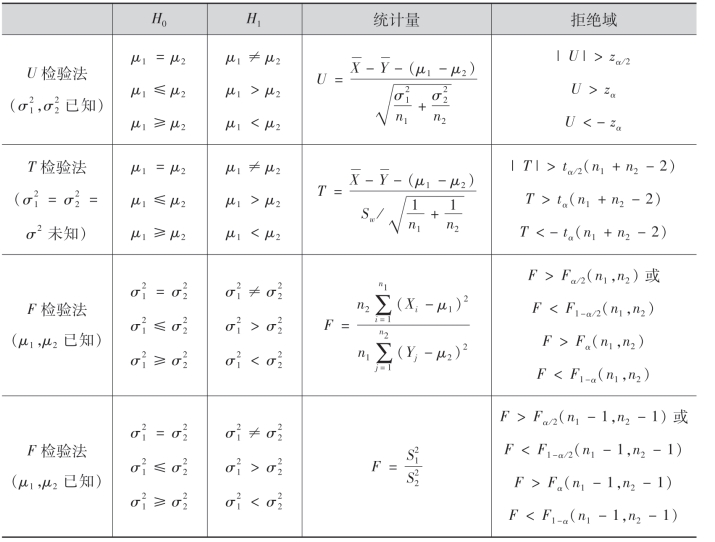
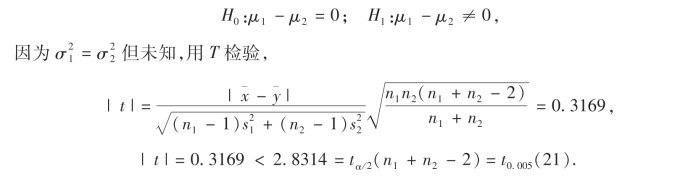
解 问题是要检验假设故接受原假设H0，即认为甲、乙两店的豆是同一类型.
注：假设用H0：μ1=μ2；H1：μ1＜μ2也可以，此时t=-0.3169＞-2.5177=-tα（n1+n2-2）仍然是接受原假设H0.
例8 改进某种金属的热处理方法，要检验抗拉强度（单位：kg/cm2）有无显著提高，在改进前的12个样品，测量并计算得¯y=28.2，（n2-1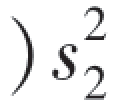
=66.64，在改进后又取12个样品，测量并计算得¯x=31.75，（n1-1）
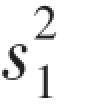=112.25，假定改进前与改进后金属抗拉强度分别服从正态分布，且方差相等，问改进后抗拉强度有无显著提高（α=0.05）？
解 依题意提出假设
由样本值算得
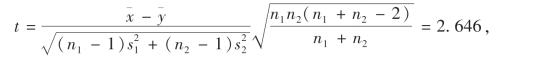
由于t=2.644＞1.717=tα（n1+n2-2）=t0.05（22），故拒绝原假设H0，即认为改进热处理方法后，抗拉强度有显著的提高.
例9 要比较甲、乙两种橡胶轮胎的耐磨性，现从甲、乙两种轮胎中各抽取8个，各取一个组成一对，再随机选取8架飞机，将8对轮胎随机配给8架飞机，做耐磨试验，飞行了一定时间的起落后，测得轮胎磨损量（单位：mg）数据如下表所示：
假定两种轮胎的磨损量分别服从正态分布，问：这两种轮胎的耐磨性能有无显著性的差异（α=0.05）？
解 将试验数据配对分析是合适的，记Z=X-Y，则
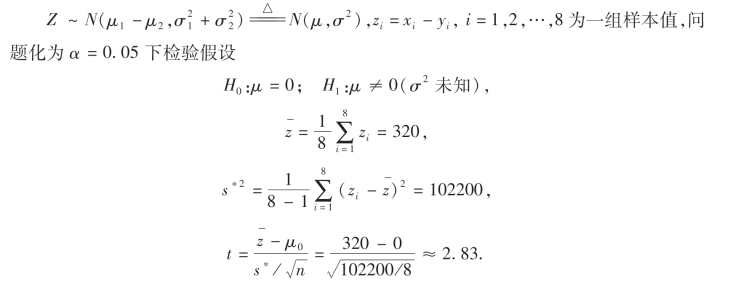
由于|t|=2.83＞2.3648=t0.025（7）=tα/2（n-1），故拒绝H0，认为耐磨损性能不同.
例10 为比较两种农药残留时间（单位：天）的长短，现分别取12块地施甲种农药，10块地施乙种农药，经一段时间后，分别测得结果为
假设两药的残留时间均服从正态分布且方差相等，试问两种农药的残留时间有无显著差异（α=0.05）.
查表得
所以在显著性水平α=0.05下接受H0，认为两种农药的残留时间无显著差异.