一、几何概率
1.几何型随机试验及其特征
概率的古典定义是在样本点个数有限且各样本点的出现具有等可能性的情况下给出的.对于样本点为无穷多的情况,概率的古典定义就不适用了,因此有必要将古典概率的定义进一步推广.下面我们来考察具有无限多个样本点而又有某种“等可能性”的类型.先看一个简单的例子.
例12 如果在一个5万平方公里的海域里有表面积达40平方公里的大陆架贮藏着石油,假如在这海域里随意选定一点钻探,问钻到石油的概率是多少?
解 由于选点的随机性,可以认为该海域中各点被选中的可能性是一样的,因而所求概率自然认为等于贮油海域的面积与整个海域面积之比,即等于![]()
这个钻探试验是一种随机试验,它代表了一类问题.这类问题的一般提法可陈述如下:
向某可度量的区域Ω内投一点,如果所投的点必在Ω内,且落在Ω中任意子区域A内的可能性大小与A的度量成正比,而与A的位置和形状无关,则称这个随机试验为几何型随机试验,或称为几何概型.
上面所说的度量,指的是有限区间的长度、可求积平面区域的面积、可求积空间区域的体积,等等.通常用μ(Ω),μ(A)分别表示区域Ω,A的度量.
2.几何概率的定义
定义3 对几何概型,若以A表示事件:“向区域Ω中随机投一点,该点落在Ω的子区域A中.”由几何概型的特征,自然应定义:
![]()
按(1.3)式定义的概率称为几何概率.
如果一个实际问题可以归结为向某区域Ω投点的问题,并且根据实际意义能够判断,所投点落在Ω中各点的可能性是一样的,则可以把它看作是几何型随机试验.
例13 (约会问题)两人约定于0到T时在某地相见,先到者等t(t≤T)时后离去,试求两人能相见的概率.
解 用x,y分别表示两人到达约定地点的时刻,问题可以看作向平面区域
Ω={(x,y)|0≤x≤T,0≤y≤T}
内投点(图1-1).由于两人分别在0到T时之间任一时刻到达约定地点是“等可能的”,故可看作几何型随机试验.
“两人能相见”这事件就是
A={(x,y)|0≤x≤T,0≤y≤T,且|x-y|≤t},
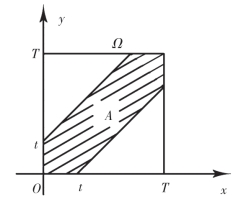
图1-1
由(1.3)式得到

例14 在长度为a的线段OM上任意投三点M1,M2和M3.试求三线段OM1,OM2和OM3能构成三角形的概率.
解 设三线段OM1,OM2和OM3的长度分别是x,y和z,则样本空间为
![]()
Ω是边长为a的立方体(如图1-2所示).记
A={OM1,OM2和OM2能构成三角形},
OM1,OM2和OM3能构成三角形的充要条件是两边之和大于第三边,即
![]()
于是
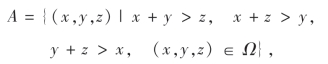
A为如图1-2所示的空间立体OBCDE,故
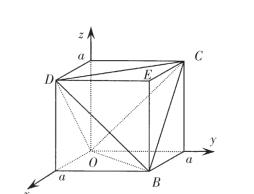
图1-2
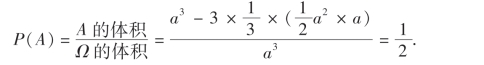
3.几何概率的性质
几何概率具有如下基本性质:
(i)非负性:对任一事件A,有
![]()
(ii)规范性:对必然事件Ω,有
![]()
(iii)有限可加性:设A1,A2,…,An为互不相容的事件,则
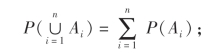
(iv)可列可加性:设A1,A2,…,An,…为可列无限多个互不相容的事件,则
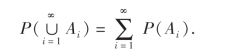
证 性质(i)和(ii)可由(1.3)式直接推得.下面证明性质(iii):
因为事件A1,A2,…,An是样本空间Ω的子区域,且它们是两两互不相容的,所以A1,A2,…,An都是可求积区域,且由度量的可加性知
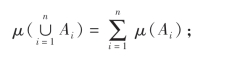
上式两端同时除以μ(Ω),得
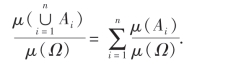
即
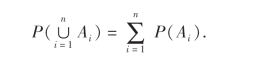
性质(iv)的证明略.
