习题二
1.(1)设随机变量X的分布律为P(X=k)=ak, k=1,2,…,n.试确定常数a.
(2)设随机变量X的分布律为
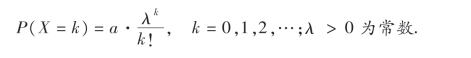
试确定常数a.
2.将红、绿、白三个球任意放到编号为1,2,3的三个盒中,设X1是放入1号盒中球的个数,X2是放有球的盒的数目,试分别求出X1和X2的分布律.
3.一个口袋中有6张卡片,分别标有-3,-3,1,1,1,2这六个数字.从这个口袋中任取一张卡片,求取得的卡片上所标数字X的分布律和分布函数.
4.将一颗骰子抛掷两次,以X1表示两次出现的点数之和,以X2表示两次出现的点数的最大者,试分别求出X1和X2的分布律.
5.箱子里装有a个白球、b个黑球.从中一次取出r个球,设其中有X个黑球,试求X的分布律.
6.一批产品中有10个合格品与3个次品.每次从这批产品中任取一件,在下列三种情况下,分别求出直到取出合格品为止所需抽取次数X的分布律.
(1)每次取出的产品不再放回;
(2)每次取出的产品仍放回;
(3)每次取出一件产品后,总以一件合格品放回该批产品中.
7.进行重复独立试验,设每次试验成功的概率为p,失败的概率为q=1-p(0<p<1).
(1)将试验进行到出现一次成功为止,以X表示所需的试验次数,求X的分布律.
(2)将试验进行到出现r次成功为止,以Y表示所需的试验次数,求Y的分布律.
8.掷一枚不均匀的硬币,出现正面的概率为p(0<p<1).若以X表示直至掷出正、反面都出现时为止所需投掷的次数,求X的分布律.
9.两名篮球队员轮流投篮,直到某人投中为止.甲队员投中的概率为0.4,乙队员投中的概率为0.6,并且甲队员先投,以X,Y分别表示甲、乙两名队员的投篮次数,试分别求X,Y的分布律.
10.电子计算机内装有2000个同样的电子管.设在某段时间内每一电子管损坏的概率等于0.0005,求在这段时间内至少有两个电子管损坏的概率(利用泊松定理计算).
11.设随机变量X服从泊松分布,且P(X=1)=P(X=2),求P(X=4).
12.设某商店每月销售某种商店的数量服从参数为5的泊松分布,问在月初要库存多少此种商品,才能保证当月不脱销的概率为0.99977.
13.设随机变量X的分布函数为
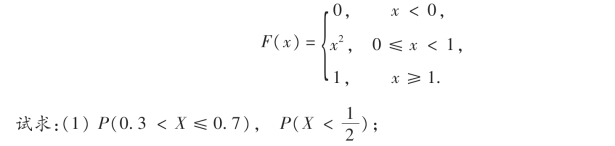
(2)X的概率密度.
14.设随机变量X的分布函数为
![]()
试求:(1)系数A,B;
(2)X落在区间(-1,1)内的概率;
(3)X的概率密度.
15.设随机变量X的概率密度为
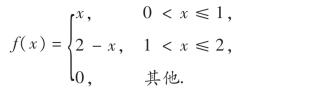
试求:(1)X的分布函数;
(2)P(X <0.5),P(X >1.3),P(0.2<X <1.2).
16.设随机变量X的概率密度为
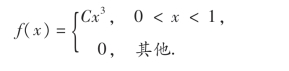
(1)确定常数C;
(2)求数a,使P(X >a)=P(X <a);
(3)求数b,使P(X >b)=0.05.
17.某种型号的电子管的寿命X(以小时计)具有如下概率密度:
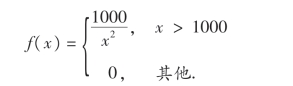
现有一大批此种型号的电子管(设各电子管损坏与否相互独立),从中任取3只,问其中至少有1只的寿命小于1500小时的概率是多少?3只电子管的寿命都小于1500小时的概率又是多少?
18.设随机变量X的概率密度为
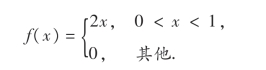
现在对X进行n次独立重复观测,以Vn表示观测值不大于0.1的次数.试求Vn的分布律.
19.设X ~N(0,1),查表计算:
(1)P(X≤0.16); (2)P(X >2.01);
(3)P(X <-1.69);(4)P(|X|<1.28);
(5)P(|X|>2.5).
20.设X ~N(-1,42),查表计算:
(1)P(X >-1.5);(2)P(X <-2.8);
(3)P(|X|<4);(4)P(-5<X <2);
(5)P(|X-1|>1).
21.某种电池的寿命服从正态分布N(a,σ2),a=300小时,σ=35小时.
(1)求电池寿命在250小时以上的概率;
(2)求x,使电池寿命在a-x与a+x之间的概率不小于0.9.
22.设X ~N(60,32),求分点x1,x2,x3,x4,使X落在(-∞,x1),(x1,x2),(x2,x3),(x3,x4),(x4,+∞)内的概率之比为7∶24∶38∶24∶7.
23.设随机变量k在区间[0,5]上服从均匀分布,求方程4x2+4kx+k+2=0有实根的概率.
24.设随机变量X的概率密度为
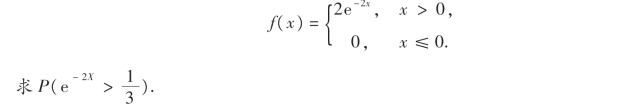
25.已知离散型随机变量X的分布律为

求Y=X2的分布律.
26.设随机变量X在区间[1,2]上服从均匀分布,试求Y=e2X的概率密度.
27.设X ~N(0,1).
(1)求Y=2X2+1的概率密度;
(2)求Y=|X|的概率密度.
28.设随机变量X的概率密度为
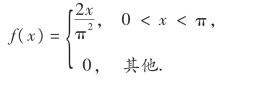
求Y=sinX的概率密度.
