小结

本章研究了极限定理，这是概率论基础中比较深入的结果，主要介绍了切比雪夫不等式、三个大数定律和两个中心极限定理.对于数理统计学的许多分支，如参数估计、假设检验、抽样调查等，中心极限定理都有着重要的作用.

在实践中，频率的稳定性是可以直接观察到的一种客观现象，贝努里大数定律则是从理论上给出这种现象更加确切的含义，即当试验次数n足够大时，事件发生的频率与概率有较大偏差的概率很小.因此，在实际应用中，当试验次数n很大时，便可用事件发生的频率近似代替事件发生的概率.由于此类定律说明了大次数的重复试验所呈现的客观规律，所以称为大数定律.

中心极限定理表明，一定条件下，大量独立随机变量和的分布趋于正态分布，这一事实说明了正态分布在概率论与数理统计中的重要性.中心极限定理揭示了为什么在实际应用中往往会遇到正态分布.另一方面，它也是保险精算等学科的理论基础之一.

假设某保险公司为某种保险推出保险业务，现有几个顾客投保，第i份保单遭受风险后损失索赔量记为Xi，对该公司而言，随机理赔量应该是所有保单索赔之和S，即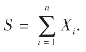弄清S的概率分布对保险公司进行保费定价至关重要.在实际问题中，通常假定所有保单索赔相互独立.这样，当保单总数n充分大时，我们并不需计算S的精确分布（一般情况下这是很困难甚至是不可能的），此时可应用中心极限定理，对S进行正态分布逼近，即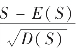逐渐向标准正态分布N（0，1）逼近，并以此来估计一些保险参数.

本章介绍的几个中心极限定理针对的是独立随机变量列的和的问题.事实上，在一定条件下，非独立随机变量之和也存在中心极限定理，这是中心极限定理研究工作者需继续研究的课题.此外，还可进一步讨论标准正态概率密度收敛的问题、正态分布收敛速度及相关问题.

想了解更具吸引力的大数定律应用范例或大数定律的精彩解释的读者，可以参考有关书籍，如《概率论及其应用》（第三版，威廉·费勒著，胡迪鹤译，人民邮电出版社，2006年）等.