小结

随机变量的分布函数完全刻画了随机变量的统计规律，它反映了随机变量的全貌，而随机变量的数字特征只是随机变量的统计规律的某一个方面的数量描述，不能完整地描述随机变量，但却反映随机变量取值的一些特性.

理解数学期望、方差的概念和性质，掌握数学期望、方差的计算.数学期望反映了随机变量X取值的平均值的大小，方差反映了X的取值与其数学期望的偏离程度的大小.在计算随机变量的期望与方差时，若分布已知，一般只需依公式计算，所要注意的是尽量利用级数求和的技巧和积分的性质；当分布未知时，一般利用关于数学期望、方差的定理和之间的关系来计算.

熟练掌握（0-1）分布、二项分布、泊松分布、均匀分布、指数分布、正态分布的随机变量的数学期望与方差的值，它们的分布函数可以完全由它们的期望和方差所确定.会根据随机变量X的分布求其函数g（X）的数学期望E［g（X）］，会根据X和Y的联合概率分布求其函数g（X，Y）的数学期望E［g（X，Y）］.

理解协方差、相关系数的概念，掌握它们的基本性质和计算.当D（X），D（Y）不变时，相关系数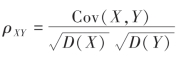反映了X和Y线性相关程度，|ρXY|愈接近1，X和Y之间愈接近线性关系；当|ρXY|=1时，X和Y之间存在线性关系Y=a+bX的概率为1；而ρXY=0，则称X与Y不相关，反映X和Y不存在线性关系，但不排除其他的联系.

理解随机变量的独立性和不相关性的概念和关系.不相关性和独立性是两个不同的概念：不相关性反映X与Y之间几乎不存在线性关系，而独立性反映X与Y取值互不影响.若X，Y独立，则X，Y不相关；若X，Y不相关，则X，Y却不一定独立；但当（X，Y）服从二维正态分布时，X和Y独立与X和Y不相关是等价的.

计算随机变量的其他数字特征的方法与计算随机变量的数学期望和方差的方法一样，一是依定义计算，但依定义计算时往往要先求随机变量的分布，这样问题会变得复杂；二是由随机变量与数字特征之间的关系来计算，这样做比较灵活简捷，但对概念与技巧的熟练程度要求较高.

本章学习的常见问题有：计算数字特征、通过数字特征确定参数、通过数字特征讨论相关性与独立性、解关于数字特征的应用题，还有一些可以作为公式应用或推广的结论的证明题.所以要求读者对数字特征的概念和性质十分熟悉，要熟谙多种解题的技巧.常用技巧有：①寻找不同概念之间的联系，由联系入手；②用“拆拼”项的手段，将原来的项组合成新项；③要善于应用级数求和与积分求积的技巧；④利用对称性、独立性、奇偶性.读者在做题时最重要还是要有开阔的思路，能进行广泛的联想，然后才能借助灵活的技巧，所以必须学会多看、多想、多实践.