均值μ的假设检验
1.σ2已知,关于μ的U检验法

然后将样本观测值代入算出U的观察值u,并比较u和zα/2,若|u|>zα/2,则拒绝假设H0(μ=μ0),这样我们便得到了检验的拒绝域W={|u|>zα/2},即


对于假设
![]()
当H0为真时,U是一个检验统计量,此时U服从N(0,1)分布,这种使用的统计量服从N(0,1)分布的检验法则称为U检验法.

同理,对于假设H0:μ≥μ0,H1:μ<μ0,对给定的显著性水平α,该检验的拒绝域应取为(-∞,-zα).
例2 设某电子产品平均寿命5000小时为达到标准,现从一批产品中抽出12件,试验结果如下:

假设该产品的寿命X ~N(μ,1400),试问此批产品是否合格?
解 由题意可知该产品寿命X ~N(μ,1400),要检验假设
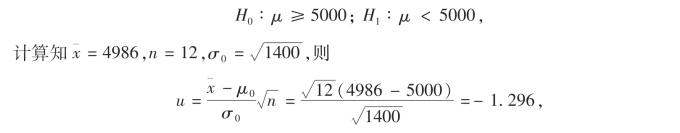
取α=0.05,查得zα=z0.05=1.645,拒绝域W={u<-zα},而此时-1.296>-1.645,故可接受H0,即认为该批产品合格.
2.σ2未知,关于μ的T检验法

这种使用的统计量服从t分布的检验法称为T检验法.
例3 今有2台仪器,对9件样品测量光谱,观察结果如下:
U(%) 0.20 0.30 0.40 0.50 0.60 0.70 0.80 0.90 1.00
V(%) 0.10 0.21 0.52 0.32 0.78 0.59 0.68 0.77 0.89
取显著性水平α=0.01,问这两台仪器测量性能有无显著差异(测量误差可看成是正态的)?
解 用X=U-V表示两台仪器测量的结果之差,则对X可看到9个结果:
![]()
可假定X ~N(μ,σ2),μ,σ2未知,由题意,要检验假设
![]()
由于σ2未知,可用T检验.此时,
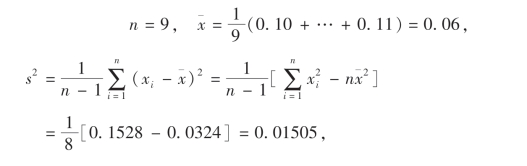
从而
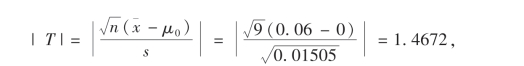
查t分位数表得tα/2=t0.005(8)=3.3554,显然,|T|<tα/2(n-1),故接受H0,认为在显著水平α=0.01下,这两台机器性能没有显著性差异.
例4 用精饲料养鸡,若干天后鸡的平均重量为4斤,今对一批鸡改用粗饲料饲养,同时改善饲养方法,经同样长的饲养期,随机抽测10只,得重量数据如下(单位:斤):
![]()
问这批鸡的平均重量是否提高了(α=0.10)?
解 由于饲养方法改善,这批鸡的平均重量是否有所提高,所以需检验假设

所以,拒绝原假设H0,接受H1,即在显著水平α=0.10下,认为这批鸡的平均重量提高了.
