* 第九章　方差分析

在生产和科研中，常常需要分析哪些因素对产品的产量、质量有显著影响，并希望知道有显著影响的因素在什么状态下能使产量、质量达到最佳的效果.例如，影响某种农作物的产量有品种、施肥量、气候、播种量等多种因素，为寻求农作物理想的生长条件，就必须在各种因素不同的状态下进行试验，并对试验结果进行分析，做出决断.解决这一问题的一个有效方法就是本章所要介绍的方差分析，它是由英国统计学家费歇尔（D.A.Fisher）建立的，并首先应用在农业试验中.后来发现其在许多研究方面有着广泛的应用，是分析试验结果的一个较好的统计方法.

在试验中，用来衡量试验效果的指标称为试验指标；对试验指标有影响的因素称为因子，一般用大写字母A，B，C等来表示；各因子所取的不同状态称为水平，因子A的各种水平可用A1，A2，…来表示.

为说明方差分析所研究的问题，我们举例如下.

例1 考察6种不同的农药，观察它们在杀虫率方面有无显著差异.由于某些因素的限制，对每种农药分别做了重复次数不相等的试验，农药的杀虫率结果如下表所示：

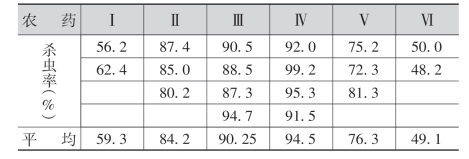
在此试验中，农药的杀虫率是试验指标，只有一个因子：农药.不同的6种农药就是这个因子的6个不同水平.从上表中我们可以看出：6种不同的农药的平均杀虫率是各不相同的，说明各种农药的杀虫率可能有显著性差异.而同一种农药的杀虫率在几次重复试验中也有较大的差异，这说明各种农药的杀虫率的差异有可能是由试验误差（由于其他未加控制的因素或不可控制的因素而产生的误差）所引起的.究竟是什么原因呢？利用方差分析就能做出明确的判断.若认为农药在杀虫率方面有显著性差异，则选用一种杀虫率较高的农药；否则，就可选用较为经济且方便的农药.

例2 某种火箭使用3种推进器和4种燃料做射程试验，对于燃料与推进器的不同组合各做了一次试验，所得火箭射程（海里）如下表所示：

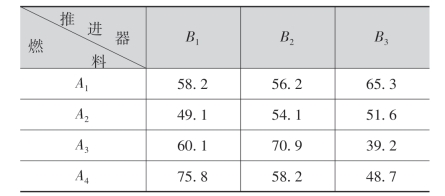
在本例中，火箭的射程为试验指标，影响试验指标的因子有：燃料A，推进器B.燃料的4个水平分别为A1，A2，A3，A4；推进器的3个水平为B1，B2，B3.试验的目的除了需要确定射程差异是由燃料的不同水平引起的，还是由推进器的不同水平所引起的之外，还需要检验燃料与推进器的不同搭配对射程是否有显著影响，从而确定最佳组合.

在例1中，只有一个因子在变化，这类试验称为单因子试验；而在例2中，有两个因子在变化，则称之为双因子试验.