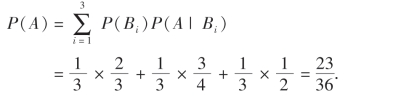乘法定理 全概率公式

二、乘法定理 全概率公式

设A，B是两个事件，P（B）＞0，则由条件概率的定义可得乘法定理：

式（1.16）可以推广到一般情形.

定理3 设n个事件A1，A2，…，An满足条件：P（A1A2A3…An-1）＞0，则有

证 因为A1A2…An-1⊂A1A2…An-2⊂…⊂A1A2⊂A1，所以

于是（1.17）式右端的诸条件概率均有意义，再由条件概率的定义可得

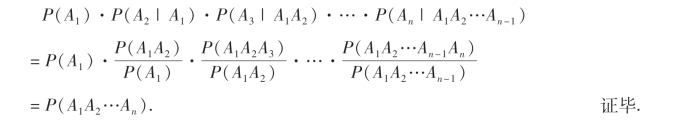
例19 箱子里有10件产品，6件是合格品，4件是不合格品.从中无放回地抽取两次，每次取一件产品，求取到的两件产品中至少有一件是不合格品的概率.

解 设A为事件“取出的两件产品中至少有一件是不合格品”，Bi为事件“第i次取出的产品是不合格品”，i=1，2.则A=B1∪B2，从而

于是所求概率为

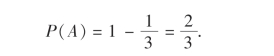
例20 设袋中装有a只红球和b（b≥3）只白球，从中连续取球4次，每次取一球，取后不放回.试求第四次才取到红球的概率.

故由乘法定理（1.17）得

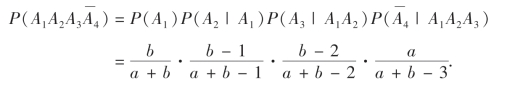
定理4 设B1，B2，…，Bn是n个互不相容的事件，且P（Bi）＞0（i=1，2，…，n），如果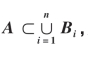则

公式（1.18）称为全概率公式.全概率公式是概率论的一个基本公式，有着多方面的应用.当事件A比较复杂，直接计算P（A）有困难时，若能找到Ω的一个划分（或满足定理4条件的）B1，B2，B3，…，Bn，且P（Bi）和P（A|Bi）为已知或比较容易计算，则可用全概率公式来求解.

例21 有3个形状相同的罐，在第一个罐中有2个白球和1个黑球，在第二个罐中有3个白球和1个黑球，在第三个罐中有2个白球和2个黑球.现任取一罐，从中任取一球，试求取得白球的概率.

解 设A表示事件“取到的是一个白球”，Bi表示事件“球取自第i罐”（i=1，2，3）.则B1，B2，B3是样本空间Ω的一个划分，且

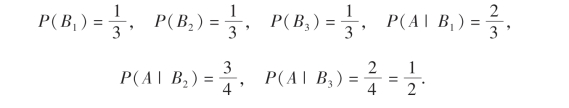
由全概率公式得到所求的概率为