协方差的定义与性质

一、协方差的定义与性质

1.协方差的定义

定义4 设（X，Y）是二维随机变量，如果

存在，则称它为X与Y的协方差，记作Cov（X，Y），即

由定义可以看出，协方差是两个变量偏差乘积的数学期望，也是一种数字特征.特别地，当X=Y时有

由于偏差可正可负，故协方差也可正可负，也可为零，当Cov（X，Y）＞0时，称X与Y正相关；当Cov（X，Y）＜0时，称X与Y负相关；当Cov（X，Y）=0时，称X与Y不相关.

计算协方差的方法通常有两种.

（1）用数学期望的定义计算：

当（X，Y）是离散型随机变量时，其联合分布律为

则

当（X，Y）是连续型随机变量时，其联合概率密度为f（x，y），则

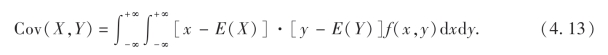
（2）直接运用下列公式计算：

事实上，

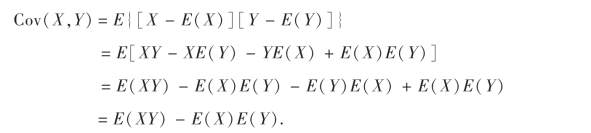
2.协方差的性质

性质1 协方差的计算与X，Y的次序无关，即

性质2 对任意常数，有

性质3 设X，Y，Z为随机变量，则

性质4 设X，Y为随机变量，则

性质5 设X与Y相互独立，则Cov（X，Y）=0，反之不然.

性质6 设X，Y为任意随机变量，则

上面性质1至4的证明较易，我们将它留给读者，下面仅就性质5，6给出证明.

性质5证明：因为X与Y相互独立，所以

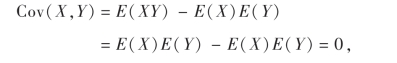
即X与Y不相关，反之不然，见下面反例.

例17 设X ～N（0，1），Y=X2，考察X与Y是否相关与独立？

解 由E（X）=0，D（X）=1，

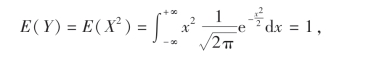
所以

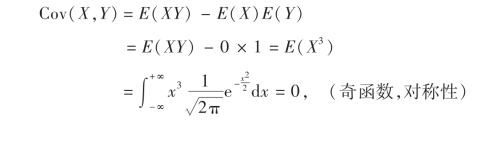
即X与Y不相关，但由于Y=X2，所以X与Y不独立.

性质6证明：根据数学期望性质7，

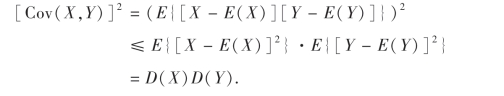
即

例18 设二维随机变量（X，Y）的联合概率密度函数为

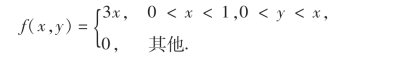
试求Cov（X，Y），并说明X与Y是否相互独立.

解

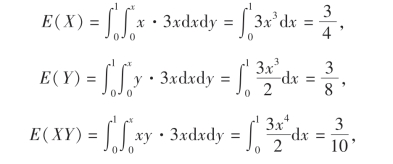
故由（4.13）式得

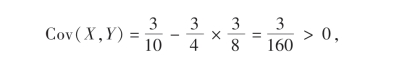
根据协方差性质5可看出X与Y不相互独立.