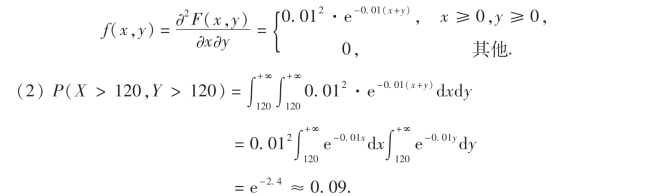二维连续型随机变量

三、二维连续型随机变量

定义4 设F（x，y）是二维随机变量（X，Y）的分布函数，如果存在非负函数f（x，y），使得对于任意x，y有

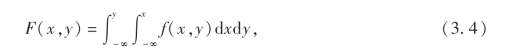
则称（X，Y）为二维连续型随机变量，并称f（x，y）为二维随机变量（X，Y）的概率密度，或称f（x，y）为随机变量X与Y的联合概率密度.

概率密度f（x，y）具有以下性质：

（1）f（x，y）≥0；

（3）设D为xOy平面上的一个区域，点（X，Y）落在D内的概率为

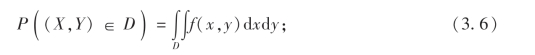
（4）若f（x，y）在点（x，y）连续，则有

最常见的二维连续型分布是均匀分布和正态分布.

二维均匀分布：设D为xOy平面上的有界区域，其面积为A，若二维随机变量（X，Y）的概率密度为

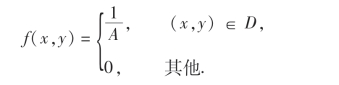
则称（X，Y）在D上服从均匀分布.

二维正态分布：若二维随机变量（X，Y）的概率密度为

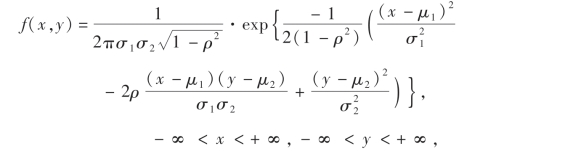
其中μ1，μ2，σ1，σ2，ρ都是常数，且σ1＞0，σ2＞0，-1＜ρ＜1，则称（X，Y）为具有参数μ1，μ2，σ1，σ2，ρ的二维正态分布，记为

例3 设二维随机变量（X，Y）的概率密度为

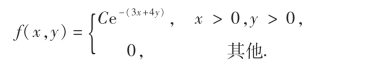
求：（1）常数C；

（2）（X，Y）的分布函数；

（3）P（0＜X≤1，0＜Y≤2）.

解 （1）由概率密度的性质有

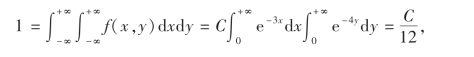
故C=12.

（2）由定义，（X，Y）的分布函数为

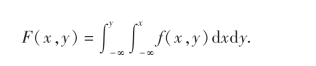
当x＞0，y＞0时，

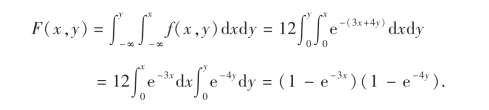
当x，y为其他情形时，F（x，y）=0，所以

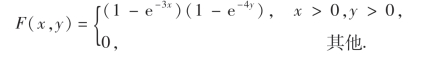
（3）由（3.1）式可得

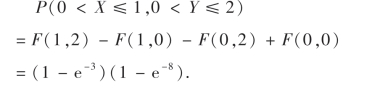
例4 一个电子器件包含两个主要元件，分别以X和Y表示这两个元件的寿命（以小时计），设（X，Y）的分布函数为

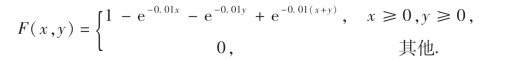
求：（1）（X，Y）的概率密度；

（2）两个元件的寿命都超过120小时的概率.

解 （1）直接验证可知F（x，y）是连续型的二维随机变量的分布函数，由（3.7）式得