§8.1 假设检验
我们可以提出许许多多的关于总体的“假设”.例如，“某门课程的考试分数服从正态分布”“我国人均身高1.75米”“某种产品是合格的”“这种药采用新配方后，疗效明显提高”，等等，这些论断在统计中称为统计假设.怎样判别一个统计假设是否成立，就需要进行随机试验，收集包含总体未知特征的数据，对数据进行分析，然后做出接受或拒绝这一假设的决策.从这个意义上讲，假设检验就是一个决策过程.
假设现有某厂生产一种灯管，其寿命X服从正态分布N（μ，40000），从过去较长一段时间的生产情况来看，灯管的平均寿命为μ=1500小时.现在采用新工艺后，在所生产的灯管中抽取25只，测得平均寿命为1675小时.问采用新工艺后，灯管寿命是否有显著提高？
我们的问题就是要判别新产品的寿命是服从μ＞1500的正态分布，还是与老产品一样服从μ=1500的正态分布.若是前者，我们说新产品的寿命有显著提高；若是后者，就说没有显著提高.
为此，我们提出统计假设：
一般情形：
这里H0表示采用新工艺后产品平均寿命没有显著增加，称为原假设；H1表示采用新工艺后新产品平均寿命有显著增加，称为备择假设.至于在两个假设中用哪一个作为原假设，哪一个作为备择假设，要看具体的目的和要求而定.假如我们的目的是希望从样本观察值对某一陈述取得强有力的支持，我们把这一陈述的否定作为原假设，而把陈述本身作为备择假设，如本例.有时，原假设的选定还要考虑到数学上的处理方便.
人们有一条普通的经验，这就是小概率事件在一次试验中不会发生.假设检验把这一条经验作为一个原则.在一次试验中若小概率事件发生了，根据以上原则，只能认为原假设是不成立的.于是我们预先指定一个小概率α，当H0为真时使得事件
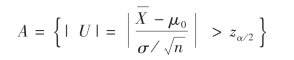
的概率为α，即
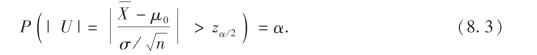
现在，根据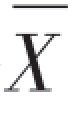
的一次观察值得出U的值，若结果|U|＞zα/2，这表明，在一次试验中小概率事件A竟然发生了，我们自然怀疑H0的真实性从而做出拒绝H0的决策.如果U的值未能使|U|＞zα/2成立，这表明小概率事件A没有发生，此时我们没有理由拒绝H0，从而做出接受H0的决策.
在本例中，若取α=0.05，则由正态分布表查得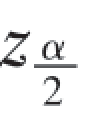
=1.96，又σ=200，n=25，由样本观察值x¯=1675，此时
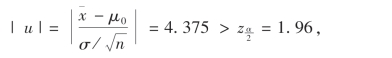
于是做出拒绝H0的决策，认为采用新工艺后，灯管寿命有明显提高.
在式（8.2）中的备择假设H1，μ的值可能大于μ0，也有可能小于μ0，称为双边备择假设，而整个检验过程称为双边检验或双侧检验.若对应的备择假设为
称为单边检验或单侧检验.在做检验时所使用的统计量称为检验统计量.当检验统计量取某一区域的值时，我们拒绝原假设H0，这个区域称为拒绝域或临界域.事先给定的数α称为检验的显著性水平.
由于检验法则是根据样本做出的，总有可能做出错误的判断.在确定了拒绝域后，取一样本，当统计量U的观察值u落在拒绝域内就拒绝H0，否则就接受H0.然而，由于样本的随机性，小概率事件并不是绝对不会发生的，当H0为真时U的值也可能会落入拒绝域，此时致使我们做出拒绝真实的H0的错误决策（弃真），这种错误称为第Ⅰ类错误.当H0为真时，U的值落入拒绝域的概率为α（由8.3式可知），因此，我们犯第Ⅰ类错误的概率就是检验的显著性水平α，即
另一方面，当H0为假时，U的值也可能落到拒绝域外，此时致使我们做出接受H0的错误决策（取假），这种错误称为第Ⅱ类错误，犯第Ⅱ类错误的概率常记为β，即
运用假设检验做推断，犯错误是难免的，但我们希望犯错误的概率小一点，也就是希望α，β的值小一点.不过在样本容量n一定时，α减少，β就会增大；反之β减少，α就会增大，要想同时减少是办不到的，适用的办法是：先确定显著性水平α的大小，然后适当增大样本容量n，以减少β，从而使α，β的值都适当小.
综上所述，当总体分布形式已知时，参数的假设检验的一般步骤如下：
（1）根据实际问题的要求，提出原假设H0及备择假设H1；
（2）给定显著性水平α及样本容量n；
（3）确定检验统计量以及拒绝域的形式；
（4）按P（拒绝H0|H0为真）=α求出拒绝域；
（5）取样本，根据样本观察值代入统计量计算确定是否拒绝原假设H0.