一、数学模型

一、数学模型

设因子A有s个水平A1，A2，…，As，在水平Aj（j=1，2，…，s）下进行了nj次独立试验，试验记录如下表所示.

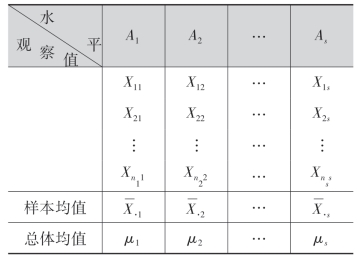
我们将在水平Aj下的试验指标视为随机变量Xj，那么在水平Aj下得到的试验结果Xij（i=1，2，…，nj）就为来自总体Xj的样本.假定总体Xj服从均值为μj、方差为σ2的正态分布，即Xj～N（μj，σ2），其中μj和σ2是需根据样本进行估计的参数，并且设不同水平Aj下的样本是相互独立的.

由于Xij～N（μj，σ2），则Xij-μj～N（0，σ2）.记Xij-μj=εij，则

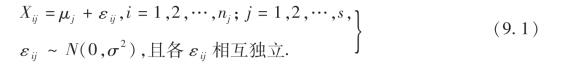
方差分析的主要任务是对模型（9.1）进行如下工作：

（1）检验s个总体Xj～N（μj，σ2），j=1，2，…s的均值是否相等，即检验假设

（2）对未知参数μj（j=1，2，…，s）和σ2做出估计.

为使检验问题写成便于讨论的形式，引进如下记号：

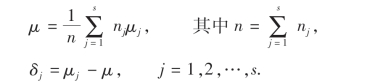
在上述记号中，μ表示μ1，μ2，…，μs的加权平均值，称之为总均值；δj反映的是在水平Aj下总体Xj的均值与总均值的差异，称之为水平Aj的效应.不难验证，下列等式是成立的：

利用这些记号，可将模型（9.1）改写成：

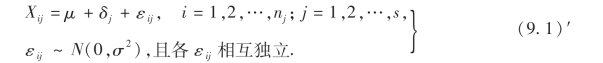
而假设（9.2）等价于如下假设：