习题七
1.设X1，X2，…，Xn为总体X的一个样本，求下述各总体的概率密度中未知参数的矩估计量：
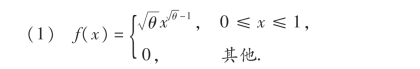
其中θ＞0，θ为未知参数；
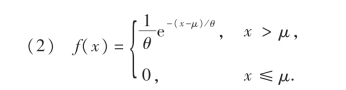
其中θ＞0，θ，μ是未知参数.
2.设X1，X2，…，Xn为总体的一个样本，求下列各总体的密度函数或分布律中的未知参数的矩估计量.
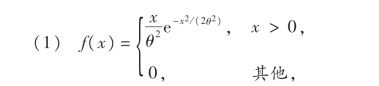
其中θ＞0，θ是未知参数.
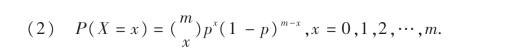
0＜p＜1，p为未知参数.
3.已知总体X的概率密度为
求参数θ的极大似然估计量.
4.一地质学家为研究密歇根湖湖滩地区的岩石成分，随机地自该地区取100个样品，每个样品有10块石子，记录了每个样品中属石灰石的石子数，假设这100次观察相互独立，并且由过去的经验知，它们都服从参数为n=10，p的二项分布，p是这地区一块石子是石灰石的概率，求p的极大似然估计值，该地质学家所得的数据如下：
5.设某种灯泡的寿命X ～N（μ，σ2），其中μ，σ2都未知，今随机抽取8只灯泡，测得寿命（以小时计）为
试估计这种灯泡使用1300小时以上的概率.
6.设T为电子元件失效时间（单位：小时），其概率密度为
假定n个元件独立地试验并已求得其失效时间分别为T1，T2，…，Tn.
（1）当t0为已知时，求β的极大似然估计量；
（2）当β为已知时，求t0的极大似然估计量.
9.设有一批产品，为估计其废品率p，随机取一样本X1，X2，…，Xn，令
10.设^θ是参数θ的无偏估计，且有D（^θ）＞0，求证（^θ2）不是θ2的无偏估计量.
并指出其中哪个最有效.
14.设X ～π（λ），λ未知，试验证样本平均值X是λ的达到方差界的无偏估计量.
15.设某种清漆的9个样品，其干燥时间（以小时计）分别为
设干燥时间总体服从正态分布N（μ，σ2），求μ的置信度为0.95的置信区间.
（1）若由以往经验知σ=0.6（小时）； （2）若σ为未知.
16.一个车间生产滚珠，从某天的产品里随机抽取5颗，测得其直径如下（单位：毫米）：
已知滚珠直径服从正态分布，求滚珠直径平均值的置信度为0.99的置信区间.
17.从自动机床加工的同类零件中抽取10件，测得其长为（单位：毫米）
已知长度服从正态分布，求方差的置信度为0.95的置信区间.
18.随机地取某种炮弹9发做试验，得炮口速度的样本标准差s=11（m/s），设炮口速度服从正态分布，求这种炮弹的炮口速度的标准差σ的置信度为0.95的置信区间.
19.随机地从A批导线中抽取4根，从B批导线中抽取5根，测得其电阻（单位：欧姆）：
A：0.143 0.142 0.143 0.137
B：0.140 0.142 0.136 0.138 0.140
设A批导线的电阻值服从N（μ1，σ2），B批导线的电阻值服从N（μ2，σ2），并且上面所得的两个样本相互独立，求μ1-μ2的置信度为0.95的置信区间.
20.研究由机器A和机器B生产的钢管的内径，随机抽取机器A生产的管子18只，测得样本方差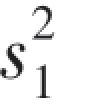
=0.34（mm）2，抽取机器B生产的管子13只，测得
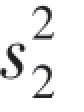=0.29（mm）2，设两样本相互独立，且机器A和B的管子的内径分别服从正态分布N（μ1，
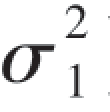），N（μ2，
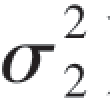），试求方差比
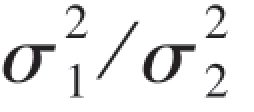的置信度为0.90的置信区间.
21.为研究某种汽车轮胎的磨损特性，随机地选择16只轮胎，每只轮胎行驶到磨损为止，记录所行驶的路程（以公里计）如下：
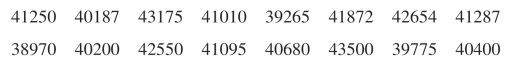
假设这些数据来自正态总体N（μ，σ2），其中μ，σ2未知，试求μ的置信度为0.95的单侧置信下限.
22.设自一大批产品的100个样品中，得一级品60个，求这批产品的一级品率的95%置信区间.
23.设总体服从指数分布，其概率密度为
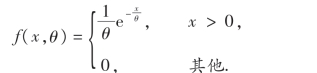
θ＞0为未知参数，从总体中抽取一容量为n的样本X1，X2，…，Xn.
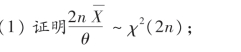
（2）求参数θ的置信度为1-α的单侧置信上限.
24.某种元件的寿命（以小时计），服从指数分布，其概率密度为
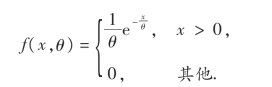
θ＞0未知，现从中抽得一容量n=16的样本，测得样本均值为5010小时，试求元件的平均寿命的置信度为0.90的单侧置信下限.