无交互作用的方差分析
在前面的例6中,我们发现因子间的交互作用并不显著,如果我们从实践中或理论上已经知道因子间无交互作用,而只需要分析各个因子的影响是否显著时,试验设计可略做修改.在每种水平搭配AiBj下只做一次试验(数据为Xij),就可对试验结果进行方差分析.由于交互效应γij=0(i=1,2,…,r;j=1,2,…,s),所以模型(9.16)可变为

这就是双因子无交互作用方差分析的数学模型.对此模型,我们提的问题就归结为检验假设:
(1)H01:α1=α2=… =αr=0; H11:α1,α2,…,αr不全为零.
(2)H02:β1=β2=… =βs=0; H12:β1,β2,…,βs不全为零.
而(9.21)式则变为
![]()
其中
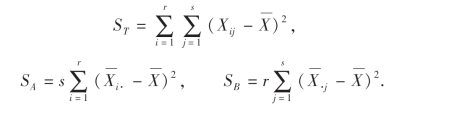
可以证明
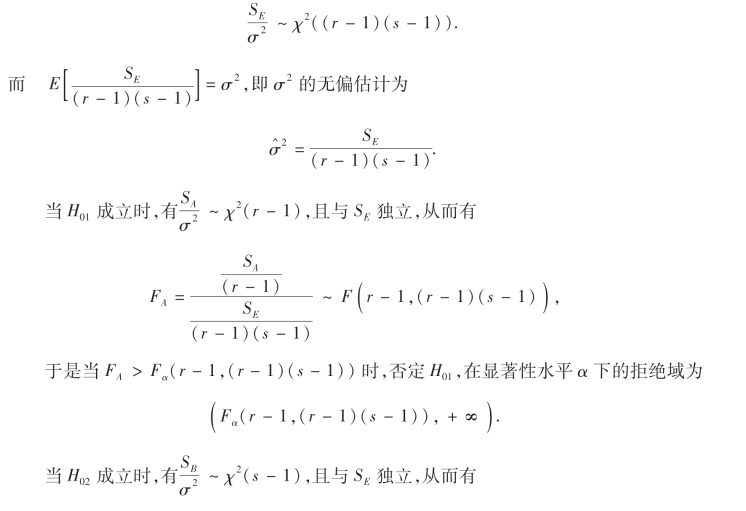
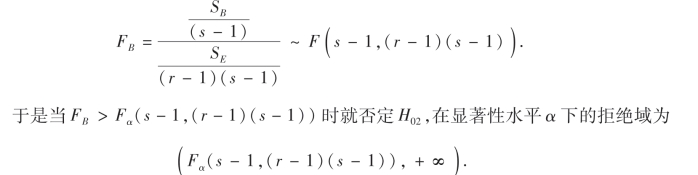
各平方和的计算公式可简化为
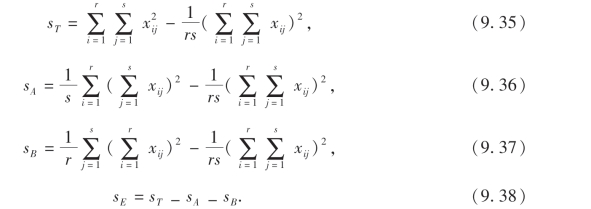
上述(9.35)~(9.38)正是(9.29)、(9.31)、(9.32)、(9.33)的特殊情形(t=1).然后计算:
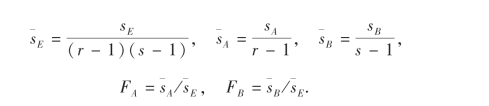
列双因子无交互作用方差分析表如下:
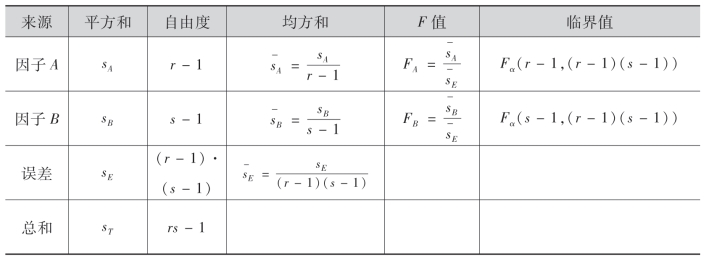
例8 为了考察蒸馏水的pH值和硫酸铜溶液的浓度(%)对化验血清中白蛋白与球蛋白的影响,将蒸馏水的pH值(A)和硫酸铜的浓度(B)分别分成4个水平和3个水平进行试验,试验结果(白蛋白与球蛋白之比)如下表所示.
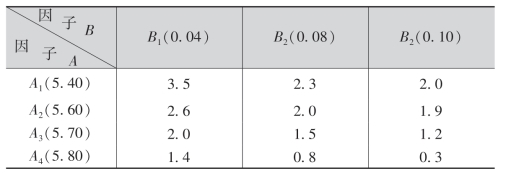
由于蒸馏水的pH值和硫酸铜的浓度无交互作用,可以假设它符合方差分析条件,试在显著水平α=0.01下检验蒸馏水的pH值和硫酸铜的浓度对白蛋白与球蛋白之比有无显著性影响.
解 r=4,s=3,计算各平方和如下:
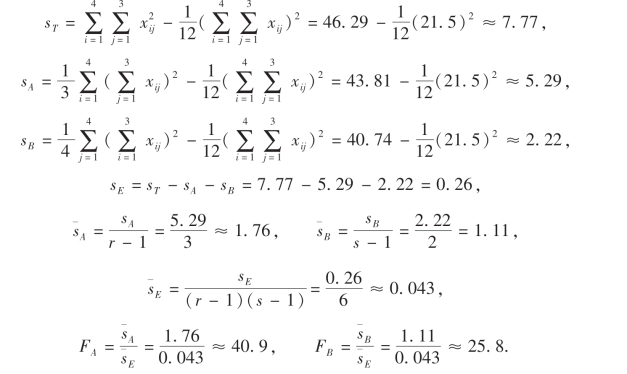
查表得F0.01(2,6)=10.9,F0.01(3,6)=9.8.列白蛋白与球蛋白之比的双因子方差分析表如下:
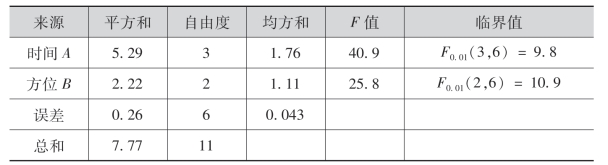
由于FA>9.8,FB>10.9,说明蒸馏水的pH值和硫酸铜的浓度对白蛋白与球蛋白之比有影响,而且非常显著.因此,在化验中一定要严格掌握蒸馏水的pH值和硫酸铜的浓度,否则就会得出错误的结果.
