习题一
1.写出下列随机试验的样本空间：
（1）观察50粒种子中发芽的粒数；
（2）一次掷两颗骰子，观察两颗骰子出现的点数之和；
（3）10只产品中有3只是次品，每次从其中取1只，取后不放回，直到将3只次品都取出，记录抽取的次数；
（4）一个小组有a，b，c，d四人，要选正式代表和列席代表各一人去参加某个会议，观察选举结果.
2.设A，B，C为三事件，试将下列事件用A，B，C表示出来：
（1）只有A发生；
（2）A，B，C都发生；
（3）A，B都发生，而C不发生；
（4）A，B，C至少有一个发生；
（5）A，B，C中至少有两个发生；
（6）A，B，C中恰好有一个发生；
（7）A，B，C中恰好发生两个；
（8）A，B，C中没有一个发生；
（9）A，B，C中至少有两个不发生；
（10）A，B，C中至多有一个发生.
3.指出下列各小题中哪些成立？哪些不成立？
（1）（A∪B）-C=A∪（B-C）；
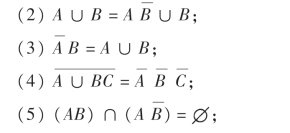
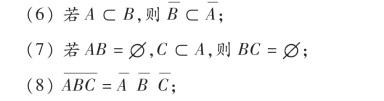
（9）若B⊂A，则AB=B，A∪B=A.
4.设Ω=｛1，2，…，10｝，A=｛2，3，4｝，B=｛3，4，5｝，C=｛5，6，7｝，用样本点表示下列事件：
5.一部五卷文集按任意次序排列到书架上，求卷号顺序自左至右或自右至左恰为1，2，3，4，5的概率.
6.房间里有10个人，分别佩戴着从1到10号的纪念章.现从这10个人中任选3人，记录其纪念章的号码，试求：
（1）最小号码为5的概率；
（2）最大号码为5的概率.
7.袋子中装有α个红球和β个黑球，从中任意地接连取出k+1（k＜α+β）个球，如果每个取出的球不放回，求最后取出的球是红球的概率.
8.袋中放有2个伍分、3个贰分和5个壹分的钱币，任取其中5个，求钱额总数超过一角的概率.
9.从5双不同尺码的鞋子中任取4只，求这4只鞋中至少有2只配成一双的概率.
10.某单位有500个员工，问至少有一员工的生日是元旦的概率是多少？（设一年按365天计算）.
11.房间里有4个人，问至少有2个人的生日是在同一个月的概率是多少？
12.袋中有n只球，分别标有号码1，2，…，n，求下列事件的概率：
（1）任意取出两球，号码是1，2；
（2）任意取出3个球，没有出现1号球；
（3）任意取出5个球，号码为1，2，3的球至少出现一个.
13.20个运动队任意分成甲乙两组（每组10队）进行比赛，已知其中有两个队是一级队，求这两个一级队：
（1）被分在不同组的概率；
（2）被分在同一组的概率.
14.在100个产品中有5个次品和95个合格品，任意从中抽取20个，求：
（1）恰有一个次品的概率；
（2）至少有2个次品的概率.
15.从（0，1）区间中随机地任取两数，求下列事件的概率：
（1）两数之和小于1.2；
（2）两数之积小于
（3）以上两个要求均满足.
16.甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头，设两船的到达时刻在一昼夜中是等可能的，且甲、乙两船停泊时间分别为1小时和2小时，求它们中任何一艘都不需要等候码头空出的概率.
21.已知三个事件A，B，C满足条件：
证明：P（AC）≥P（A）P（C）.
22.证明：若P（A|B）＞P（A），则P（B|A）＞P（B）.
23.将一颗均匀的骰子连掷两次，设A表示事件“两次掷出的点数之和为10”，B表示事件“第一次掷出的点数大于第二次掷出的点数”，试求P（B|A）和P（A|B）.
24.某种动物由出生算起活到20岁以上的概率为0.8，活到25岁以上的概率为0.4，问现年龄为20岁的这种动物活到25岁以上的概率是多少？
25.设P（A）=α，P（B）=β＞0，证明：
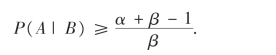
26.已知在10个晶体管中有2个次品，在其中任取两次，每次取一个做不放回抽样，求下列事件的概率：
（1）两个都是正品；
（2）两个都是次品；
（3）一个正品，一个次品；
（4）第二次取到的是次品.
27.两批相同种类的产品各有12件和10件，每批产品中各有一件废品，现在先从第一批产品中任取一件放入第二批中，然后再从第二批中任取一件，求这时取到废品的概率.
28.袋子中装有编号分别为1，2，…，n的n个球.先从袋中任取一球，如取到的是1号球就不放回袋中，如不是1号球就放回袋子中；然后再取一球，求这时取到2号球的概率.
29.有2个箱子，甲箱中有3只白球和2只黑球，乙箱中有2只白球和5只黑球，任选一个箱子，并从中任取一球，求此球是白球的概率.
30.已知男人中有5%是色盲患者，女人中有0.25%是色盲患者，今从男女人数相等的人群中随机地挑选一人，恰好是色盲患者，问此人是男性的概率是多少？
31.一个工厂有甲、乙、丙三个车间生产同一种螺钉，每个车间的产量分别占总产量的25%，35%，40%，并且设它们的次品率分别是5%，4%，2%.现在从它们混合在一起的产品中任取一个，发现是次品，问该次品是甲、乙、丙车间生产的概率各是多少？
32.设8支枪中有3支未经试射校正，5支已经试射校正，一射击手用校正过的枪射击时，中靶的概率为0.8，而用未校正过的枪射击时，中靶的概率为0.3.射击手从这8支枪中任取一支进行射击，结果中靶，求所用的这支枪是校正过的概率.
33.已知事件A，B相互独立，且两个事件仅发生A的概率或仅发生B的概率都是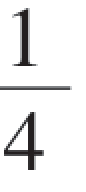
，求P（A）和P（B）.
34.已知
，证明事件A与B是相互独立的.
35.设事件A，B，C是总体相互独立，求证：
（1）A∪B，AB，A-B都与C相互独立；
（2）
也是总体相互独立.
36.设事件A在四次重复独立试验中至少发生一次的概率为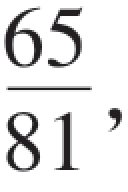
，求事件A在一次试验中发生的概率.
37.甲、乙、丙三人独立地破译一份密码，已知各人能译出的概率分别为
问三人中至少有一人能将此密码译出的概率是多少？
38.进行n次重复独立试验.设事件A在每次试验中发生的概率为p.试求A在第n次试验中发生，且在前n-1次试验中发生k-1次的概率.
39.甲、乙、丙三人同时对飞机进行射击，三人击中的概率分别为0.4，0.5，0.7.飞机被一人击中而被击落的概率为0.2，被两人击中而被击落的概率为0.6，若三人都击中，飞机必定被击落.求飞机被击落的概率.