随机变量的函数的数学期望

三、随机变量的函数的数学期望

从上面随机变量的数学期望的定义可以看出，在求随机变量的数学期望时，应该先求出该随机变量的分布律或概率密度函数.但在理论研究和实际应用中却经常遇到求随机变量X的函数Y=g（X）的数学期望的问题，按定义应先求出Y=g（X）的分布，然后再利用Y的分布求E（Y），这样做显然比较麻烦.其实，我们也可以直接利用随机变量X的分布律或概率密度函数求E（Y），为此给出下面的定理.

定理1 设Y为随机变量X的函数，即Y=g（X），其中g为连续的实函数.

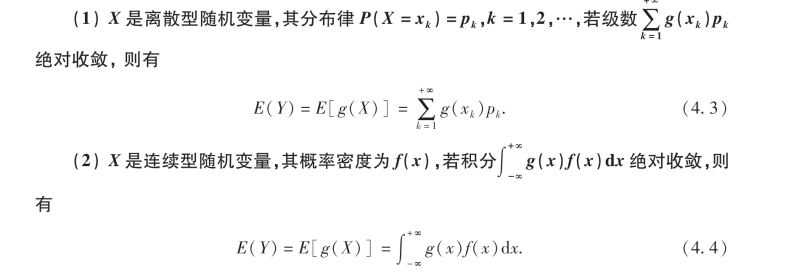
证略.

上述定理可以推广到两个或两个以上随机变量的函数的情形，现针对求二维随机变量函数的数学期望叙述该定理.

定理2 设Z=g（X，Y）是二维随机变量（X，Y）的函数，其中g为连续的实函数.

（1）当（X，Y）是二维离散型随机变量时，其分布律为

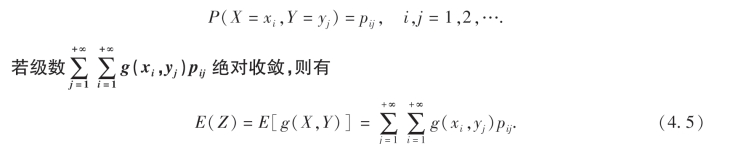
特殊地

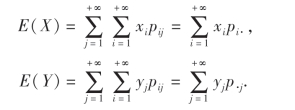
特殊地

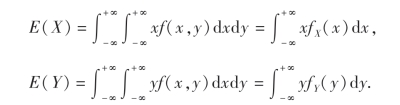
上述公式能避免计算随机变量的函数的分布而直接求数学期望，在多数情况下非常有用.

例6 设随机变量的分布律为

求E（-2X+1），E（X2）.

解 由（4.3）式，得

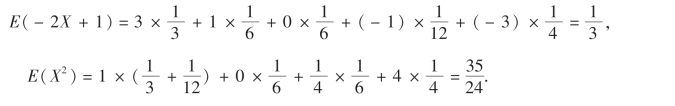
例7 设二维随机变量（X，Y）在区域D=｛（x，y）|0≤x≤1，0≤y≤x｝上服从均匀分布，求E（X），E（Y），E（XY）.

解 （X，Y）的概率密度函数为

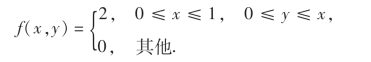
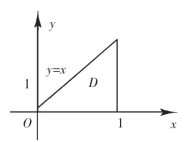
图4-1

由（4.6）式，得

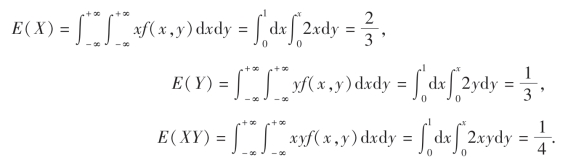
该题也可以先求边缘概率密度函数fX（x），fY（y），然后再求E（X），E（Y），读者可自己尝试.