二、检验方法
类似于单因子方差分析，我们需要构作一个统计量，使其既能反映出因子A，B的效应大小，又能反映出交互作用A×B的效应大小.构作的方法也与单因子时一样，可以从总偏差平方和中分解出来，为此，先引进一些记号：
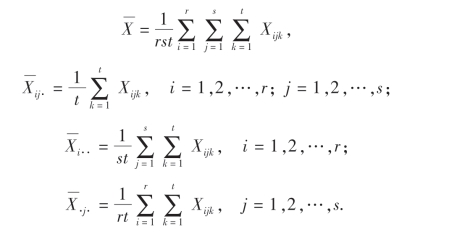
不难证明，未知参数μij，μi·，μ·j及μ的无偏估计为
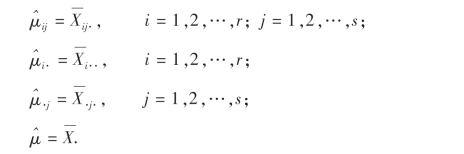
并且可得效应γij，αi，βj的无偏估计为
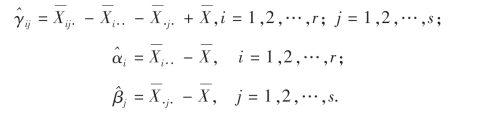
只要稍做验证，我们还可以发现这些估计满足下列关系：
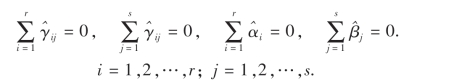
下面我们来推导总偏差平方和的分解式：
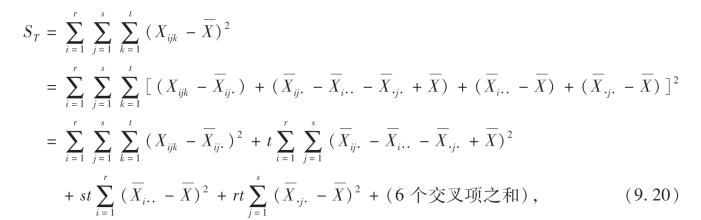
而上式中的6个交叉项均为0，例如：
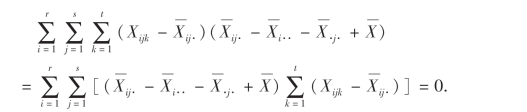
记
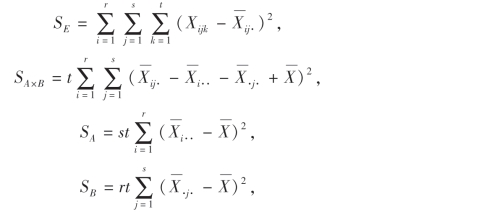
则（9.20）式就表示为
其中ST表示总偏差平方和，SE表示误差平方和，SA×B表示A与B的交互效应平方和，SA为因子A的效应平方和，SB为因子B的效应平方和.容易证明：
当假设H01成立时，有
且与SE独立；
当假设H02成立时，有
且与SE独立；
当假设H03成立时，有
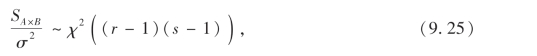
且与SE独立.
这样得检验方法如下：
（i）当假设H01成立时，
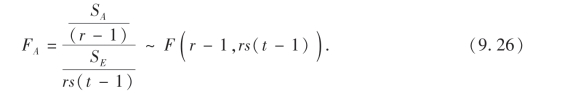
所以，对于给定的显著性水平α，拒绝域为
即当FA＞Fα（r-1，rs（t-1））时，否定假设H01，认为因子A有显著性影响.
（ii）当假设H02成立时，
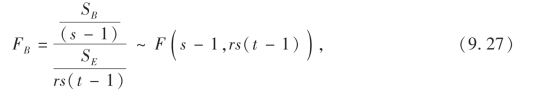
故对于给定的显著性水平α，拒绝域为
即当FB＞Fα（s-1，rs（t-1））时，否定假设H02，认为因子B有显著性影响.
（iii）当假设H03成立时
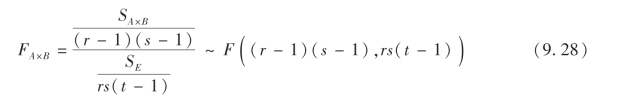
在显著性水平α下，拒绝域为
ST的自由度为rst-1，SA的自由度为r-1，SB的自由度为s-1，SA×B的自由度为（r-1）（s-1），SE的自由度为rs（t-1）.按公式（9.26）、（9.27）、（9.28）分别计算FA，FB，FA×B的值，再与相应的临界值Fα比较，就可做出推断.
最后，将所得的结果，列双因子方差分析表如下：
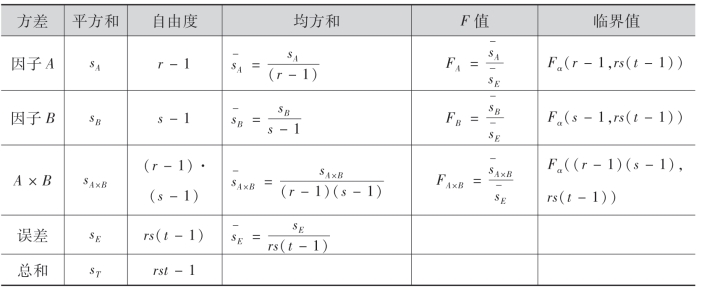
在做具体计算时，各平方和一般按如下公式进行计算：
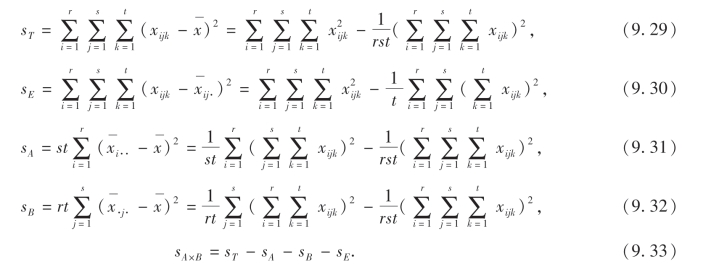
例6 某铀矿床地下水中铀含量不仅随季节有所变动，而且随层位深度也有所波动.对水中铀含量的这种波动，究竟是季节不同引起的，还是层位深度引起的，或者是两者共同作用造成的影响.仅仅凭一般的观测很难得出结论.为此，在某地的钻孔内，按月进行定深取样，测得地下水铀含量（%）如下表所示，试在显著性水平α=0.05下，检验不同月份、不同层位深度以及它们的交互作用对地下水的铀含量是否有显著性影响？
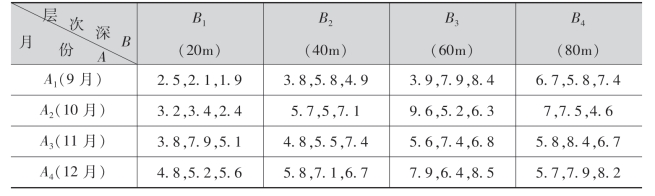
解 r=s=4，t=3，按（9.29）至（9.33）的公式可计算各平方和如下：
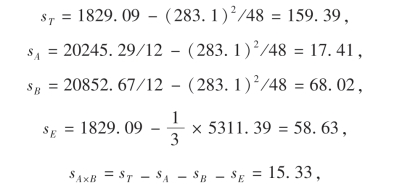
且
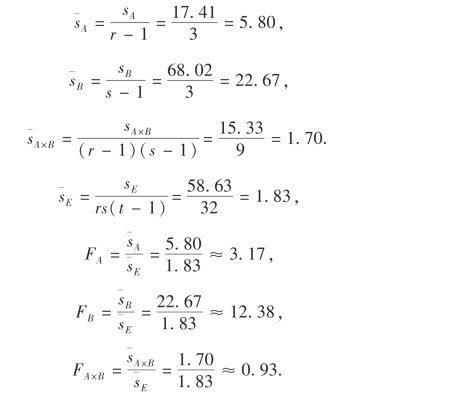
由上述结果，得地下水铀含量方差分析表如下：
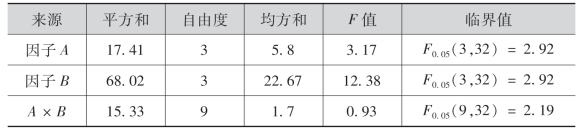
续表
由表中可看出，FA＞F0.05（3，32），FB＞F0.05（3，32）.这说明因子A及因子B对铀含量均有显著性影响，且因子B的影响则更为突出；FA×B＜F0.05（9，32），则说明两因子的交互作用对铀含量的影响并不显著，或者说没有交互作用.
在实际应用中，一般先计算FA×B，对交互作用进行检验，如果交互作用不显著，则将A×B一栏的平方和与自由度分别加到误差栏中去，重新计算FA，FB，以新的FA，FB对因子A，B进行检验.在本例中，因FA×B＜F0.05（9，32），则需重新计算：
可见FA，FB略有增加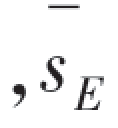
稍有减小，因子A与因子B的显著性有所提高.
例7 某种火箭用4种燃料、3种推进器做射程试验，在试验中，对燃料和推进器的各种水平组合均进行了2次发射试验，射程数据在下表中给出：
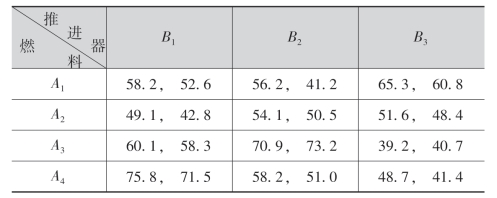
试分析燃料、推进器以及它们的交互作用对射程有无显著性影响.设显著性水平α=0.01.
解 r=4，s=3，t=2，各平方和计算如下：
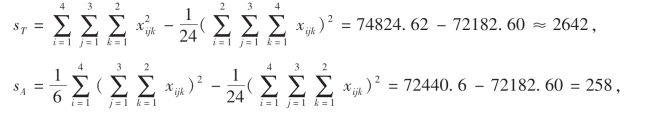
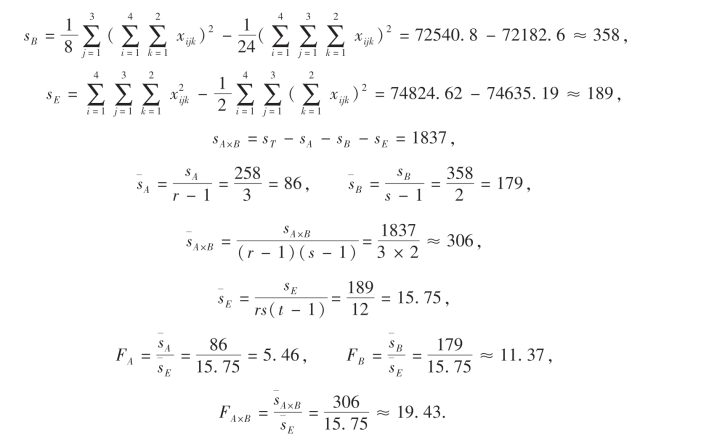
于是可得射程试验方差分析表如下：
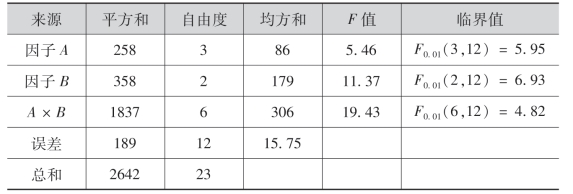
FA＜F0.01（3.12），说明因子A对射程无显著性影响；FB＞F0.01（2，12），FA×B＞F0.01（6，12），则说明因子B以及A，B的交互作用对射程均有显著性影响，并且以交互作用对射程的影响最为显著.
