二、检验方法
对假设检验问题(9.2)或(9.2)′做出推断,事实上就是回答因子是否对试验指标有显著性影响,我们是根据样本来做出推断的.为寻求检验(9.2)或(9.2)′的统计量,需要分析造成试验数据Xij波动的原因.由(9.1)式知,试验数据Xij的差异显然是由如下两个方面的因素引起的:一是由试验误差εij所引起;二则可能是由于假设(9.2)或(9.2)′不真所引起.这就要求我们构造一个样本的函数,使得这个函数既能反映出试验误差的大小,又能反映出所讨论的因子各水平效应的大小.

事实上,
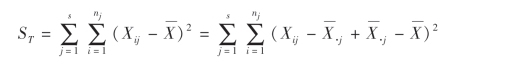
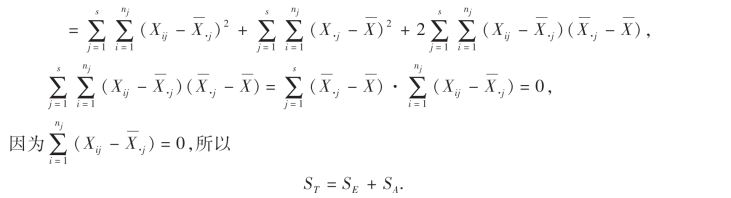
由(9.3)式可知,当效应平方和SA越大,误差平方和SE就越小.现在的问题是SA大到什么程度,SE小到何种程度时,可以认为因子A的各水平间有显著性差异呢?这就要求我们进一步讨论SA和SE所满足的分布规律.
将SE表成如下形式:
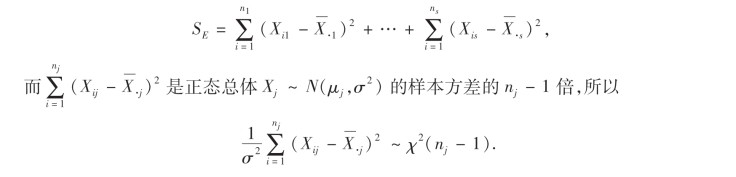
因为各Xij相互独立,所以SE中各平方和也相互独立,由χ2分布的可加性,有

从而SE的自由度为n-s,且
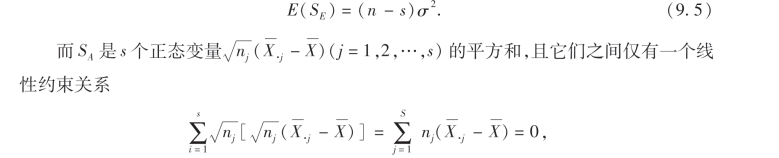
所以SA的自由度为s-1.注意到
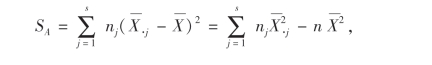
且
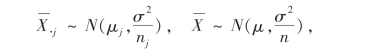
不难推出
![]()
进一步还可证明:当假设H0为真时,SA与SE相互独立,且

所以当H0为真时,比值

的观察值F0应在1的右边接近于1.若F0过大,则假设H0就可能不真.(9.8)式就是我们检验H0所需要的统计量.它是两个方差的比给出的,方差分析便由此得名.由(9.4)式、(9.7)式以及SA与SE的独立性知,当H0为真时,
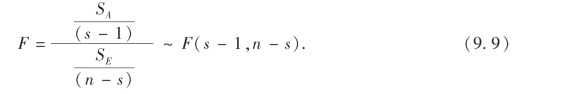
由此可见,当因子水平间差异越大时,比值F也越大,当根据样本值算出F的观察值F0大于临界值Fα(s-1,n-s)时,就否定假设H0,认为因子对试验指标有显著性影响.这里α是事先给定的显著性水平,临界值Fα(s-1,n-s)可在书后所附的F分布表中查得.
当H0为真时,因为所有的Xij~N(μ,σ2),且相互独立,所以

即ST的自由度为n-1.
综上讨论,我们把检验方法归纳如下:
(1)根据下列公式计算ST,SE,SA的观察值sT,sE,sA:
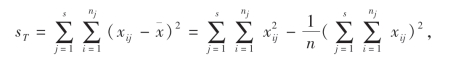
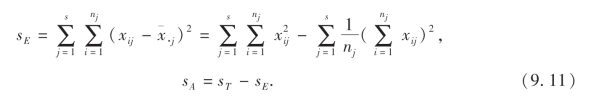
(2)计算F的观察值F0:

(3)对给定的显著性水平α,在F分布表中查得临界值Fα(s-1,n-s),若F0>Fα(s-1,n-s),则说明因子对试验指标有显著性影响.否则认为因子对试验指标没有显著性影响.拒绝域为(Fα(s-1,n-s),+∞).
(4)为便于在实际中使用上述分析结果,一般列单因子方差分析表如下:
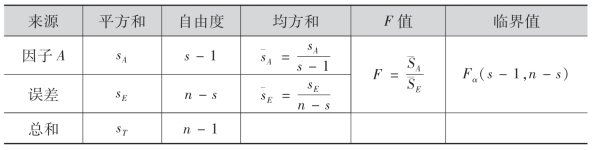
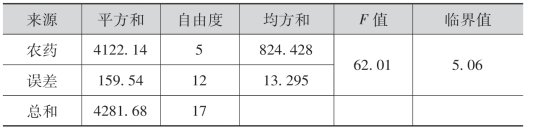
例3 在例1的农药试验中,试检验6种不同的农药在杀虫率方面是否有显著性差异(α=0.01).
解 这里:s=6,n1=2,n2=3,n3=4,n4=4,n5=3,n6=2.
而
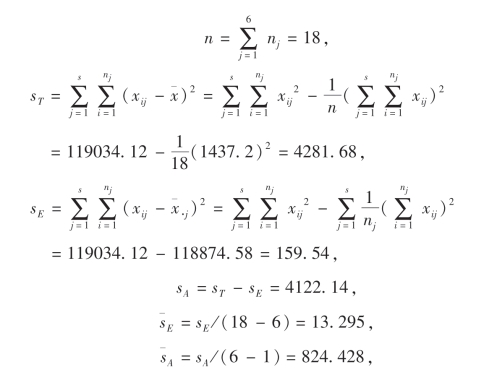
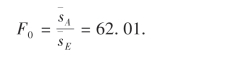
临界值F0.01(5,12)=5.06.
所以F0>F0.01(5,12),有显著性影响,即不同的6种农药在杀虫率方面有显著性差异.列方差分析表如下:
这是一个不等重复试验.我们再讨论一个等重复试验的例子.
例4 某灯泡厂用4种不同配料方案制成的灯丝,生产了4批灯泡.在每批灯泡中随机地抽取7个灯泡测其使用寿命(单位:小时),数据列于下表:
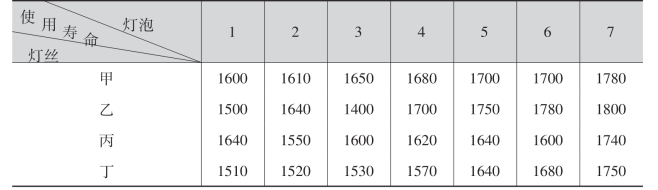
试问这四种灯丝生产的灯泡的使用寿命有无显著性的差异?
解 若以μ1,μ2,μ3,μ4分别表示这四种灯丝生产的灯泡的使用寿命的总体均值,则要检验假设为
![]()
这里:s=4,n1=n2=n3=n4=7.
而
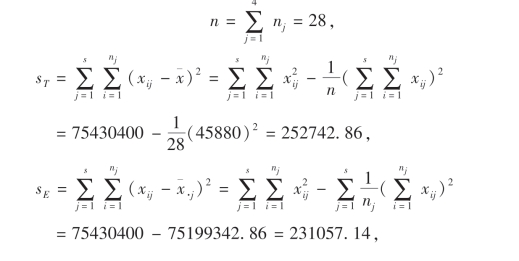
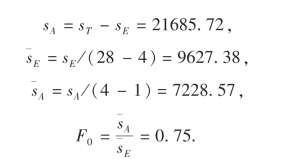
查表得F0.01(3,24)=4.72,F0.05(3,24)=3.01.由此可得如下方差分析表.
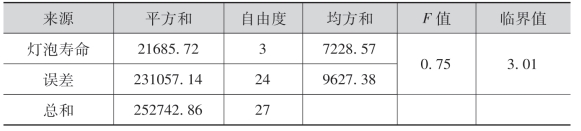
由于F0<F0.05(3,24),所以没理由拒绝H0,即这4种灯丝生产的灯泡的使用寿命没有显著性的差异.在实际工作中,通常说这个因子对试验指标的影响不显著,灯丝的4种配料方案质量相当,则可选取成本较低的配料方案.
注:若F0>F0.01,则称因子A的影响高度显著,若F0.01≥F0>F0.05,则称因子A的影响显著;若F0≤F0.05,则称因子A的影响不显著.
在上述两例中,例3是不等重复试验,即nj≠nk(存在j,k,1≤j≠k≤s);例4是等重复试验,即n1=n2=… =ns=r,n=s·r.从上述两例中,我们首先可以看出不等重复试验比等重复试验在计算上更为麻烦.另外,在试验总次数n固定不变时,等重复试验的精确度比不等重复试验的精确度更高.在例3中,设试验总次数仍为18,而每种农药均重复做3次试验,那么精确度将得到提高.因此,我们提倡在分析实际问题时,尽可能采用等重复试验.
