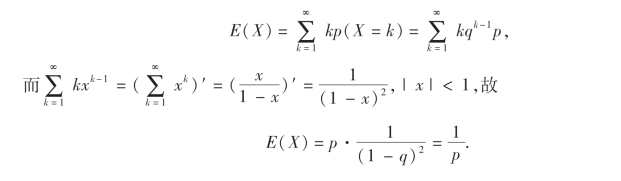离散型随机变量的数学期望

一、离散型随机变量的数学期望

为了说明什么是数学期望，先看一个例子，某战士在20次射击中的成绩如下：

问该战士的射击水平如何？

人们常常根据“平均中靶环数”来对射手的射击水平做出综合评价，记平均中靶环数为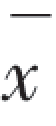，则有

或者写成下面的形式

定义1 设离散型随机变量X的分布律为

例1 设随机变量X ～B（n，p）（二项分布），求E（X）.

解 X的分布律为

由（4.1）式，得

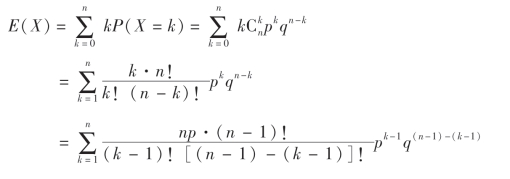
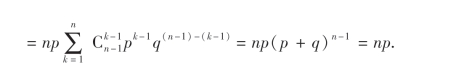
显然当n=1时，X服从（0-1）分布（二点分布），E（X）=p.

例2 设随机变量X ～π（λ）（泊松分布），求E（X）.

解 X的分布律为

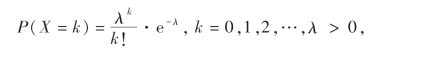
由（4.1）式，得

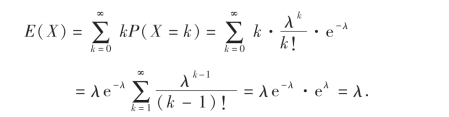
例3 某流水生产线上每个产品不合格的概率为p（0＜p＜1），各产品合格与不合格相互独立，当出现一个不合格产品时即停机检修，设开机后第一次停机时已产生了的产品个数为X，求X的数学期望E（X）.

解 根据题设，知X ～G（p）（几何分布），其分布律为

由（4.1）式，得