频率分布和直方图

二、频率分布和直方图

设总体X是一个连续型随机变量.下面介绍一种根据样本观察值x1，x2，…，xn来近似地求总体X的概率密度函数f（x）的图解法——直方图法.

把区间（a，b］分成r+1个小区间（t0，t1］，（t1，t2］，…，（tr，tr+1］.

区间的长度都为

r的大小一般随样本容量n而定，n小时，r也应小些；n大时，则r也应大些.

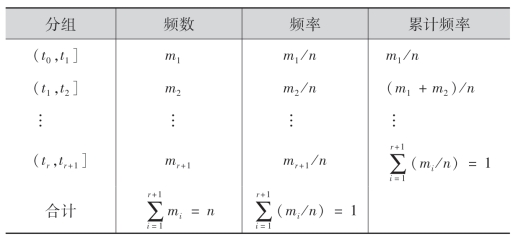
算出样本观察值落入第i个小区间（ti-1，ti］的个数（即频数），记为mi，称为样本观察值落入第i个小区间（ti-1，ti］的频率，i=1，2，…，r+1.列频率分布表：

在xOy平面的上半平面上画一排矩形，即对于每个i（1≤i≤r+1），作出以x轴上的区间（ti-1，ti］为底，以为高的矩形（图6-1）.这样的图就叫作频率直方图.

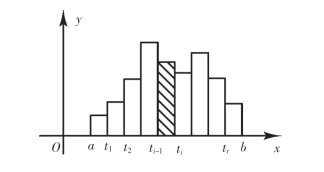
图6-1

假设pi表示随机变量X落入（ti-1，ti］的概率，根据概率的统计定义可知，当n充分大时，vi稳定地在常数pi附近摆动，即

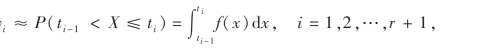
其中f（x）为X的概率密度函数.

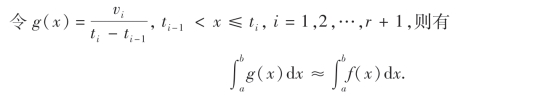
由此可见，根据频率直方图得到的函数g（x），可作为总体X的概率密度函数的一种近似.因此，只要有了频率直方图，就可以大致画出概率密度函数的曲线.