两个事件的独立性
定义6 设A，B是两个随机事件，如果P（A）＞0，且有
则称事件B关于事件A是独立的.
B关于A独立的含义是事件B的概率不受附加条件“事件A已发生”的影响.
例24 袋中有10张卡片，分别标有数字0，1，2，…，9，每次从中任意抽取一张，取后放回，共取两次.以A表示事件“第一次取到标有奇数的卡片”，B表示事件“第二次取到的卡片上所标数字小于3”.验证事件B关于事件A是独立的.
证 样本空间Ω=｛（i，j）|i，j=0，1，…，9｝，其中（i，j）表示“第一次取到的卡片上标有数字i，第二次取到的卡片上标有数字j”.A=｛（i，j）|i=1，3，5，7，9；j=0，1，2，…，9｝，B=｛（i，j）|i=0，1，2，…，9；j=0，1，2｝，AB=｛（i，j）|i=1，3，5，7，9；j=0，1，2｝.由于是古典型随机试验，且Ω，A，B，AB中包含的样本点个数分别为100，50，30，15，所以
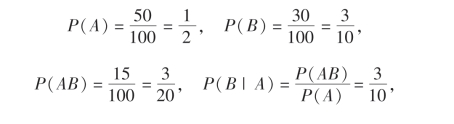
即有
故事件B关于事件A是独立的.证毕.
由于是有放回抽样，第一次取卡片的情况对第二次取卡片的情况没有影响，所以有上面得到的结论.
定理6 设A，B是两个随机事件，若P（A）＞0，则事件B关于事件A独立的充要条件是
证 若事件B关于事件A独立，即P（B|A）=P（B），则由乘法定理得
P（AB）=P（A）P（B|A）=P（A）P（B）.
反之，若P（AB）=P（A）P（B），由于P（A）＞0，所以
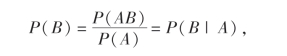
由定义知事件B关于事件A是独立的.证毕.
推论 设A，B是两个随机事件，P（A）＞0，P（B）＞0，则事件B关于事件A独立当且仅当事件A关于事件B独立.
证 由定理6，当P（A）＞0，P（B）＞0时，B关于A独立⇔P（AB）=P（A）P（B）⇔A关于B独立.证毕.
由此可见事件A和B之间的独立性是相互的.
稍微注意一下就知道，定理6中的关系式（1.21）比定义6中的关系式（1.20）有几个明显的优点：
（i）它不必用到条件概率的概念；
（ii）它在形式上关于A，B是对称的；
（iii）当P（A）=0或P（B）=0时，（1.21）式仍然成立.
这是因为当P（A）=0或P（B）=0时，P（A）P（B）=0，且
从而有
注意这时条件概率P（B|A）或P（A|B）无意义.因此，如果把关系式（1.21）作为事件A，B之间的独立性的定义，则不但使定义的表达更简洁，而且还把定义的适用范围稍许推广.
定义6′ 设A，B是两个随机事件，如果
则称事件A和B是相互独立的.
定理6告诉我们，当P（A）＞0时，定义6与定义6′其实是一致的.后面我们将采用定义6′.
另外，容易验证，任一事件A与不可能事件
是相互独立的；任一事件A与必然事件Ω也是相互独立的.
证 因为
所以
于是
由定理7可知，若式（1.20）成立，0＜P（A）＜1，则
即不论事件A发生与否，事件B发生的概率都一样.
例25 考虑向正方形区域ABCD内投一质点的几何型随机试验.令E，F，G，H为正方形各边的中点（图1-3）.设M1表示事件“质点落在矩形AFHD内”，M2表示事件“质点落在矩形ABGE内”，M3表示事件“质点落在三角形ABD内”，试讨论M1，M2，M3两两之间的独立性.
解 由于是几何型随机试验，故
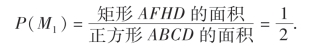
同理
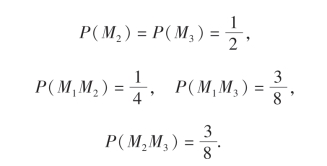
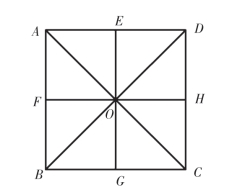
图1-3
由定义6′立即看出：M1和M2相互独立，M1与M3不独立，M2与M3不独立.