概率的古典定义与实例
定义2 若在某随机现象的试验中共有n个等可能的样本点，而随机事件A是由其中的m（0≤m≤n）个样本点所组成，则事件A的概率是
概率的古典定义与统计定义是一致的.事实上，若设Ω=｛ω1，ω2，…，ωn｝为古典型随机试验的样本空间，A是含有m个样本点的事件（A⊂Ω），即A=｛ωi1，ωi2，…，ωim｝.由于每个样本点出现的可能性相等，而事件的统计概率是反映事件发生的可能性大小的客观度量，所以各样本点的统计概率应相等.由统计概率的性质
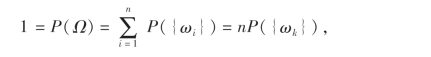
即
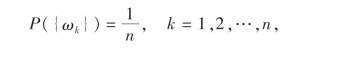
从而
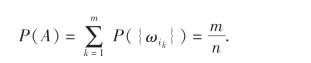
这就说明事件A的统计概率与古典概率是相等的.
例7 将一颗均匀的骰子掷两次，观察其先后出现的点数.设A表示事件“两次掷出的点数之和为5”，B表示事件“两次掷出的点数中一个恰是另一个的两倍”.试求P（A）和P（B）.
解 随机试验的样本空间为
其中（i，j）表示“第一次掷出的点数为i，第二次掷出的点数为j”这一样本点.Ω中包含36个样本点，且由骰子的对称性知，每个样本点发生的可能性相同.因为A=｛（1，4），（2，3），（3，2），（4，1）｝，B=｛（1，2），（2，4），（3，6）（2，1），（4，2），（6，3）｝，所以由（1.1）式，得
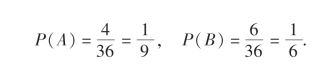
计算古典概型中事件A的概率时，如果样本点较多或问题比较复杂，一般不再将Ω中的样本点全列出来，而只需分别求出Ω中与A中所包含的样本点的个数，再由（1.1）即可求出A的概率，但这常需要利用排列与组合的知识.
例8 随机地将15名新生平均分配到三个班级中去，这15名新生中有3名是优秀生，试问：
（1）每个班级各分配到一名优秀生的概率是多少？
（2）3名优秀生分在同一班级的概率是多少？
解 设 A1=｛每个班级各分配到一名优秀生｝，
A2=｛3名优秀生分在同一个班级｝.
先从15名新生中选5名分配到第一个班级有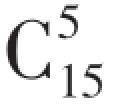
种分法，然后从剩下的10名新生中选5名分配到第二个班级有
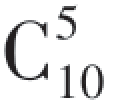种分法，剩下的5名新生分配到第三个班级，故由乘法原理知样本点总数为
·
·
.
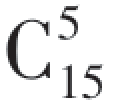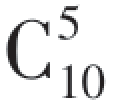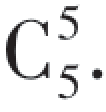例9 箱子里有N件产品，其中有N1件正品和N2件次品（N1+N2=N），从中任意抽取n件产品，求事件“抽出的n件产品中有n1件正品（n2=n-n1件次品）”A的概率，抽取方式为
（1）有放回抽取（每次取一件，取后放回；再任取一件，共取n次）；
（2）无放回抽取（每次取一件，取后不放回，共取n次，相当于一次抽取n件）.
（2）无放回抽取时，样本点是从N个元素中选取n个的选排列，即ω=（a1，a2，…，an）.因此样本点总数为
同理，事件A所含样本点个数为
显然各样本点的出现是等可能的，故
例10 将n个人随机地分配到N（n≤N）个房间里，每个房间容纳的人数不限.试求下列各事件的概率：
（1）A：“某指定的n个房间中各有一人”；
（2）B：“恰有n个房间，其中各有一人”；
（3）C：“某一指定的房间中恰有k人”.
解 由于每个人都可分配到N个房间的任一间，所以将n个人分配到N个房间里去有Nn种分法，每一种分法是一样本点，即样本点有Nn个.由于分法的任意性，各样本点的出现是等可能的.
（1）将n个人分配到指定的n个房间，每个房间一人，共有n！种分法，即A含有n！个样本点，故
（2）由于n个房间可以是任意的，即是从N个房间中随机选出来，其选法共有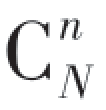
种；对于每选定的n个房间，每一房间分配一个人的方法有n！种，故B包含的样本点个数为
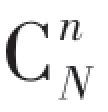·n！，于是得到
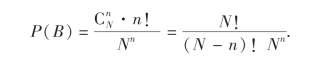
（3）指定房间分配的k人可以从n个人中任意选出，有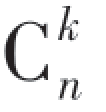
种选法，剩下的n-k人可以任意分配到其余的N-1个房间，有（N-1）n-k种分法，故C包含了
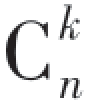·（N-1）n-k个样本点，所以
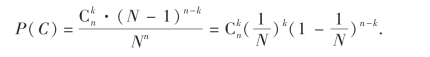
例11 袋中有a个红球、b个白球，现在把球随机地一个个摸出来，求第k次摸出的一个球是红球的概率（1≤k≤a+b）.
解 以A表示事件“第k次摸出的一个球是红球”这一事件.把a个红球及b个白球都看作是不同的（比如设想它们都编了号），若把摸出的球依次放在排列成一直线的a+b个位置上，则可能的排列法相当于把a+b个元素进行全排列.将每一种排列法作为一个样本点，那么各样本点的出现是等可能的，样本点总数为（a+b）！，下面求事件A所包含的样本点个数，由于第k次摸得红球有a种取法，而另外（a+b-1）次摸球相当于a+b-1个球进行全排列，有（a+b-1）！种方法，故事件A所包含的样本点个数为a×（a+b-1）！.于是
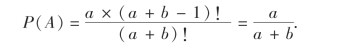
这个结果与k无关，它与我们日常生活中的经验是一致的.例如，在体育比赛中进行抽签，对各队机会均等，与抽签的先后次序无关.