二、无偏性

二、无偏性

由于估计量是样本的函数，样本的抽取具有随机性，对于不同的样本值就会得到不同的估计值，所以估计量也是一个随机变量.当然我们希望估计值在未知参数的真值左右徘徊，并且使它的数学期望与未知参数的真值相等，这就是无偏性标准的基本思想.

证 设X的一个样本为X1，X2，…，Xn，则有

由前面知识，有

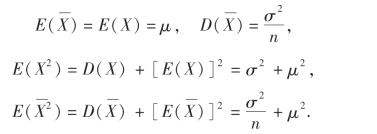
又

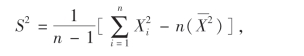
所以

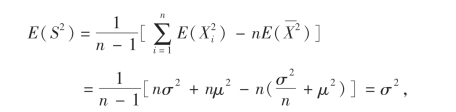
即有

所以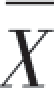，与S2分别是参数μ和σ2的无偏估计量.

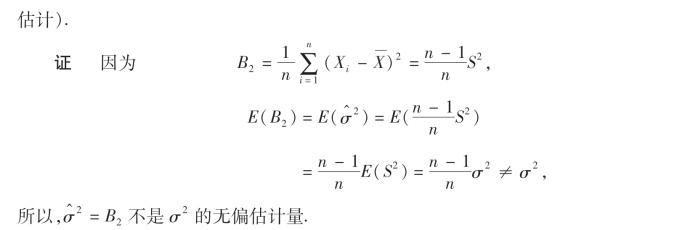
上面两个例子说明，样本方差S2和样本二阶中心矩B2都是总体方差σ2的一致估计量，但S2是σ2的无偏估计量，B2是有偏的.因此，我们一般取样本方差S2作为总体方差σ2的估计量.我们还可以证明：不论总体服从什么分布，k阶样本（原点）矩Ak是k阶总体（原点）矩μk的无偏估计量.

值得指出的是，同一未知参数可以有不同的估计量，而且还可以有不同的无偏估计量.举例如下：

例10 总体X服从参数为θ的指数分布，概率密度为

所以，L=Xi（i=1，2，…，n）也是θ的无偏估计量，即X1，X2，…，Xn中的任何一个都可以作为θ的无偏估计量.